Greedy
반응형
탐욕 알고리즘이라고도 불린다.
재귀, 분할정복과 dp처럼 특정 문제를 해결하기 위한 알고리즘이라기보다는, 문제 해결에서 사용할 수 있는 도구 중 하나라고 생각하면 좋을 것 같다.
여러 가지 경우 중 하나를 결정해야 할 때, 선택의 순간마다 최적이라고 판단되는 케이스를 선택하는 방향으로 진행해 최종 값을 산출하는 알고리즘이다.
그리디 알고리즘을 사용해서 풀 수 있는 대표적인 문제로, 부분 배낭 문제가 있다.
무게 제한이 있는 상황에서, 최대 가치를 담을 수 있도록 배낭에 물건을 넣어야 한다.
물건들에 대한 무게와 가치 정보가 주어진다.
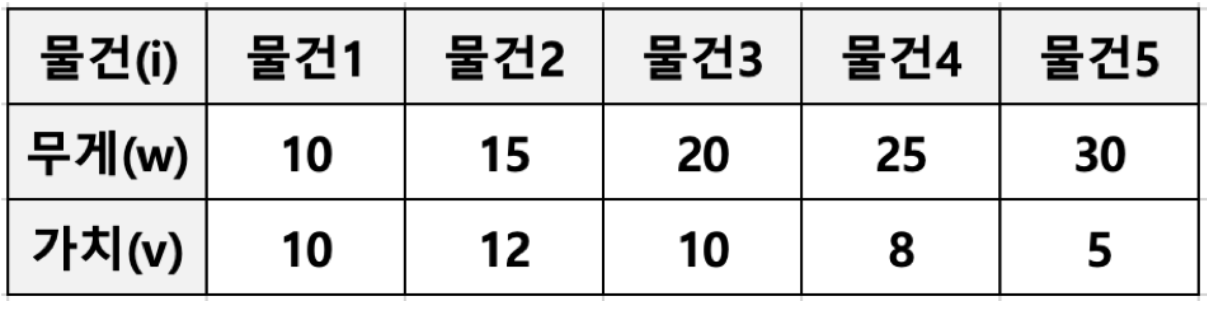
여기서, 물건을 쪼개서 넣을 수 있다면 분할 가능 배낭 문제 (Fractional knapsack problem)이고, 쪼갤 수 없으면 knapsack problem이라고 말한다.
일단, 각 물건에 대한 정보를 담기 위해 2차원 배열을 생성하자.
그 다음 가장 효과적인 물건을 설정해야 한다.
가치를 무게로 나누면 대략적으로 물건의 효율성을 알 수 있다.
그리디 알고리즘 구현을 위해 Comparator를 활용해 효율성을 기준으로 배열을 정렬한 후 배낭에 물건을 넣자.
public class GreedyAlgorithm {
public void knapsackFunc(Integer[][] objectList, double capacity) {
double totalValue = 0.0;
double fraction = 0.0;
// Fraction Knapsack
Arrays.sort(objectList, new Comparator<Integer[]>() {
@Override
public int compare(Integer[] objectItem1, Integer[] objectItem2) {
return (objectItem2[1] / objectItem2[0]) - (objectItem1[1] / objectItem1[0]);
// 물건의 효율성을 기준으로 정렬한다. 내림차순.
}
});
for (int index = 0; index < objectList.length; index++) {
if ( (capacity - (double)objectList[index][0]) > 0 ) {
capacity -= (double)objectList[index][0];
totalValue += (double)objectList[index][1];
// 담을 수 있으면 담는다.
} else {
fraction = capacity / (double)objectList[index][0];
totalValue += (double)objectList[index][1] * fraction;
break;
// 담을 수 없으면 쪼개서 담는다.
}
}
}
}
그리디 알고리즘이 항상 최선의 결과를 도출하는건 아니다.
선택의 순간에서 눈 앞에 보이는 상황만 비교해서 더 좋은 쪽으로 선택할 뿐, 이어서 찾아올 결과에 대해서는 고려하지 않는다.
반응형
'Algorithm > Theory && Tip' 카테고리의 다른 글
| 최단 경로 - 다익스트라 (0) | 2022.04.13 |
|---|---|
| Backtracking (0) | 2022.04.11 |
| DFS (0) | 2022.04.06 |
| BFS (0) | 2022.04.06 |
| 이분탐색 (0) | 2022.04.04 |
댓글
이 글 공유하기
다른 글
-
최단 경로 - 다익스트라
최단 경로 - 다익스트라
2022.04.13 -
Backtracking
Backtracking
2022.04.11 -
DFS
DFS
2022.04.06 -
BFS
BFS
2022.04.06