Linear Model - Classification
지난 시간에 Supervised Learning에서의 Linear Model을 Regression문제에 적용했었다.
Regression을 배웠으니 Classification에 적용해보자.
1. Binary Classifier / Logistic Regression
2. Softmax Classifier / Multinomial Logistic Regression
Classifier기술은 Regression기술에 의존해 만들어졌기 때문에 Classifier 모델이지만 Logistic Regression처럼 Regression 용어가 쓰인다.
1. Binary Classifier / Logistic Regression

Regression 모델로 접근하면 공부 시간에 따른 점수를 예측할 수 있다.
위의 그림처럼 H(x)를 만들고 점수를 예측할 수 있는데 이 모델과 Classification 모델이 어떤 연관이 있을까?
Classification 모델로 접근 시 공부 시간에 따른 어떤 시험에 대한 Pass / Fail을 예측할 수 있다.
이 문제를 위의 Regression 모델로 해결하려 하면 여러 문제가 발생한다.
(Bound 문제가 대표적임)
그래도 위의 H(x)모델이 아예 의미가 없지는 않은데, 점수에 따라서 0~50점은 fail을, 51~100점은 pass를 주고 싶다고 하면 위의 모델을 어느정도 이용할 수 있을 것이다.
위의 모델을 기반으로 하면서 H(x)를 0과 1사이로 매핑하는 함수가 뭐가 있을지 찾아봤다.

Sigmoid 함수, 혹은 Logistic 함수라고 불리는 함수이다.
수학 가형을 응시한 수험생이라면 낯설지 않게 다가올 함수인데, 이 함수로 0 ~ 1 사이 값을 매핑할 수 있다.
H(x)를 구하고 위의 함수에 합성시켜 원하는 결과를 얻는다.
z값이 음의 무한대로 뻗어나간다고 하면, g(z)값은 0으로 수렴하고 양의 무한대로 뻗어나간다고 하면 g(z)의 값은 1로 수렴한다. 그리고 z값이 0 이라면 1/2값을 가진다.
0 <= g(z) <= 1 이라는 반경을 가지고 있는 함수여서, 이 함수와 어떤 함수를 합성해도 반경은 변하지 않는다.
그리고 이 함수는 도함수(Derivate)가 존재하는데, 이는 Gradient Descent와 관련이 있음을 말한다.
결국 이 Logistic function을 가져다가 딥러닝 같은곳에 활용할텐데, 학습을 위해서는 Gradient Descent방식을 꼭 활용하게 된다.
이 도함수를 가진다는 조건은 매우 중요한데, 사실 미분가능하다는 조건이 필요없다면 y=x와 같은 간단한 함수로도 비슷한 역할을 할 수 있다. 일단 여기서는 도함수를 가진다는 조건이 매우 중요함을 알고 넘어가자.
아 그러면 이 함수로 다 해먹을 수 있겠구나~ 라고 생각할 수 있다.
하지만 생각처럼 그렇지 않다. 처음 이 함수가 나왔을 때는 세상의 주목을 받고 많이 활용됐다. 하지만 사용해보며 성능이 그렇게 좋지 못하다는 점을 발견하고 여러 학자들이 이 함수를 대체할 수 있는 다양한 함수들을 만들어내고, 이런 함수들을 토대로 다양한 토대로 학문이 발전해나갔다.
정리해보면
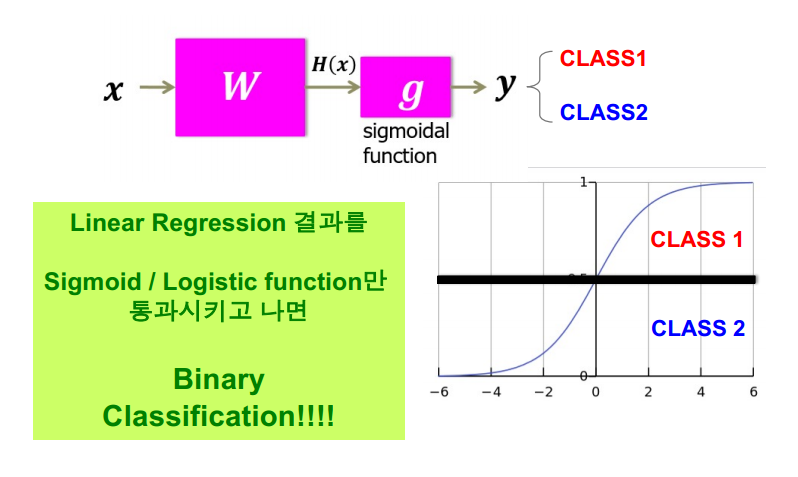
x를 구하고 Wx+b라는 H(x)를 구한다.
g(z)함수에 H(x)함수를 합성한다.
그리고 기준을 하나 정하고 그 기준보다 크면 class1 작으면 class2 로 구분한다.
즉, Linear Regression결과를 Logistic function을 통과시키면 Binary Classification 모델을 만들 수 있다.
그런데, 이렇게 Binaray Classification 모델은 두 가지 클래스에 대해서만 구분할 수 있다.
세 가지 이상의 클래스를 구분할 때는 어떻게 해야 할까?
2. Softmax Classifier / Multinomial Logistic Regression

공부한 시간과 출석에 따라 학점 A B C를 예측하는 문제를 해결해보자.
먼저, 이진 분류기를 계속 사용해 문제를 해결할 수 있어 보인다.
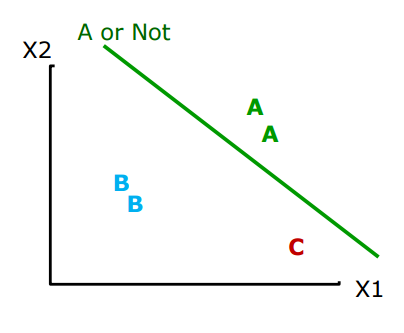

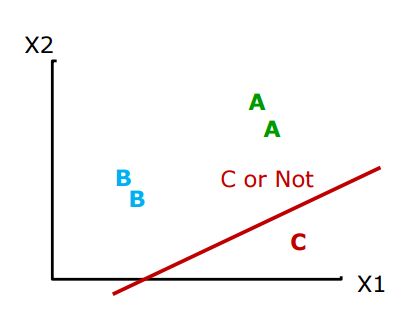
위와 같이 표현할 수 있다.
x 값을 구하고, (x1,x2) 각 성적에 따른 W와 b를 구한다. 그 값을 Logistic function에 집에넣고 결과를 얻는 방식으로 진행한다.
하지만 이렇게 클래스를 분류하게 되면
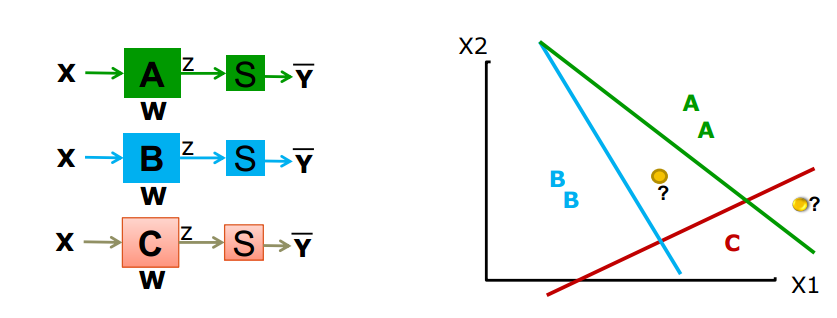
위와 같이 어떤 클래스에 위치해야 하는지 구별할 수 없는 경우가 생긴다.
일단 얻은 결과를 Linear System으로 표현해보면
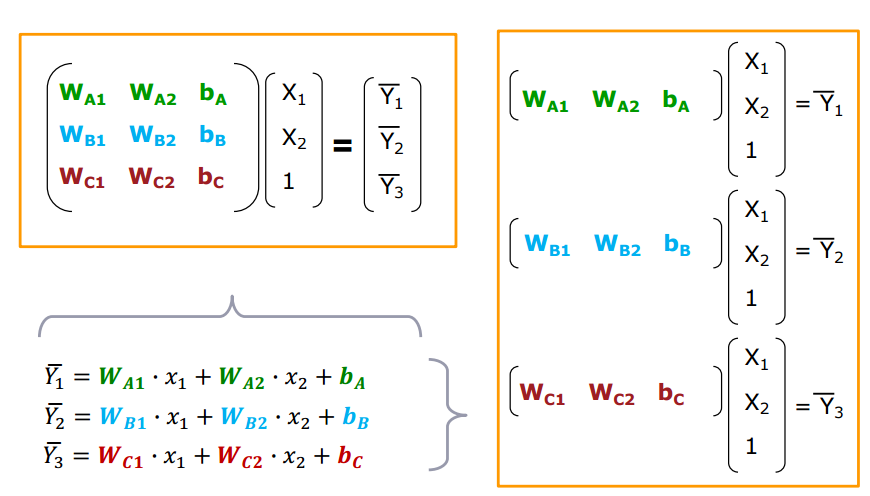
위와 같이 표현된다. (벡터 형태로 표현할 때 상수값에는 1이 붙음)
행렬 형태에서 3*3 행렬은 Model Parameter이고 3*1 행렬의 Data 결과값은 Predicted Score를 의미한다.
즉 다시 정리하면
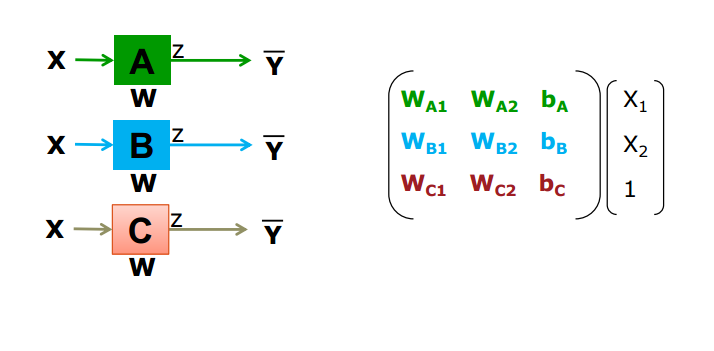
x값을 구하고 W와b를 설정한 다음 결과를 낸 상태이다.
우리는 A B C 성적을 매기는 해결책을 구하고 있다.

이처럼 결과값이 주어졌다고 해보자.
(아직 Logistic Function을 통과시키지 않아서 결과값이 0~1사이가 아니다.)
이 결과값을 Softmax Function에 적용시켜보자.

softmax함수는 0~1사이의 값으로 정규화하는 함수인데, 위의 식에서 함수의 동작을 살펴보면
x값인 [2,1,0.1]을 통해 주어진 함수를 통과시키고 결과값을 얻는다. (깔끔하게 소숫점 첫째 자리까지 표현함)
softmax 함수를 통해 정규화한 각각의 합은 1이 되고 이 값들을 확률값으로 생각하자.
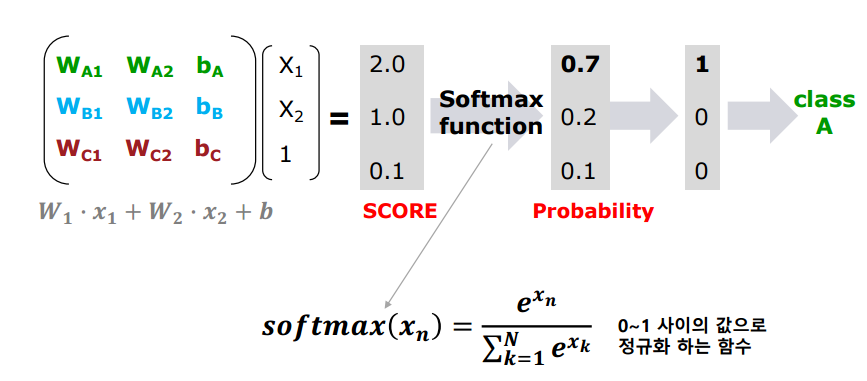
x값 -> W,b값 -> Score -> 확률값 -> 클래스 구분
위의 절차로 문제를 해결한다.
Classification 문제가 Regression문제와 아예 다르지 않다는 걸 보여준다.
위의 예시는 세 가지 성적에 대해 구분했는데, 그 이상의 가짓수도 당연히 성립하고 나아가 복잡한 이미지 인식에도 사용될 수 있다.
Multinomial Logistic Regression = Softmax Classifier
'Machine Learning > AI Introduction' 카테고리의 다른 글
| Deep Learning (1) (0) | 2021.11.14 |
|---|---|
| Machine Leaning - Overfitting (0) | 2021.10.24 |
| Machine Learning - Unsupervised Learning (0) | 2021.10.17 |
| Machine Learning - Supervised Learning (5) (0) | 2021.10.17 |
| Machine Learning - Supervised Learning (4) (0) | 2021.10.17 |
댓글
이 글 공유하기
다른 글
-
Deep Learning (1)
Deep Learning (1)
2021.11.14 -
Machine Leaning - Overfitting
Machine Leaning - Overfitting
2021.10.24 -
Machine Learning - Unsupervised Learning
Machine Learning - Unsupervised Learning
2021.10.17 -
Machine Learning - Supervised Learning (5)
Machine Learning - Supervised Learning (5)
2021.10.17