[UPL] Syntax & Parsing
프로그래밍 언어는 문자열의 집합이고, 프로그래밍 언어로 작성된 프로그램은 문자열이라고 생각할 수 있다.
그렇다고 아무 문자열이나 프로그래밍 언어가 될 수 있는 건 아니다. 특정 문법에 부합해야 프로그래밍 언어가 될 수 있다.
문자열 s가 프로그래밍 언어인지 판단하는 함수 L(G) 를 생각해보자.
s가 L(G)의 집합에 포함된다면 s는 프로그래밍 언어라고 할 수 있다.
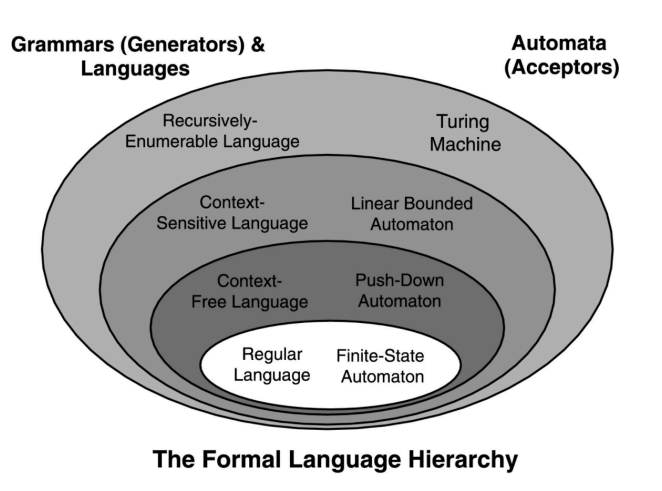
위의 Chomsky Hierarchy는 언어의 표현력을 나타낸다.
사실상 튜링 머신은 존재하지 않고 Regular Language는 프로그래밍 언어를 정의할 때 표현력이 부족해 독립적으로 사용되지 않으니 프로그래밍 언어의 정의는 두 가지로 구분된다.
오토마타는 문자열 s가 L(G) 집합에 포함되는지를 판단한다.
Lemail 언어를 집합으로 정의한다고 하자. 원소나열법으로는 무한집합을 정의할 수 없으니 조건제시법을 사용해야 한다.

정규표현식 (Regular Expression)으로 정규언어를 정의해보자.


언어 정의에서 공집합은 이 언어에 원소가 하나도 없음을 의미하고, 빈 문자열은 길이가 0인 문자열을 의미한다.
연산자 간에는 Kleene > Concat > Union 순으로 우선순위가 있으니 괄호로 우선순위를 표현해주자.
Extended Regular Expression을 사용해 Regular Expression보다 식을 간결하게 표현할 수 있다. (+ ? n-to-m times)


Finite State Automata는 유한한 상태를 가지는 추상 기계로 s가 Regular Language에 속하는지 판별할 때 사용한다.
전이함수, 시작 단계, 종료상태를 잘 확인하고 문자열을 한 글자씩 읽어 전이시켜보자.
Regular Expression은 Finite State Automata로 변환할 수 있고, 반대도 성립한다.

Abstract Syntax Tree가 만들어지기 전 까지는 Frontend, 뒷 부분 부터는 Backend로 구분된다.
Syntax를 Tree구조로 만드는 이유는 트리 순회를 통해 최적화나 정적 분석을 효과적으로 수행할 수 있기 때문..
Lexical Analysis 단계는 문자열을 입력받아 프로그래밍 언어의 어휘항목(토큰)으로 잘라내는데, 이 단계에서 Regular Expression을 사용한다.
Finite State Automata는 상태 수가 고정되어 있어 입력을 기억할 수 없다.
L = {a^n b^n | n>=1} 이런 언어는 n이 100인 경우 a를 100개 읽고 b를 100개 읽어야 하는데.. a를 100개 읽은 상태를 기억할 수 없어서 Finite State Automata로 표현할 수 없다.
Context-Free Language는 문맥 자유 언어로 동일 단어가 문맥을 고려하지 않고 항상 같은 뜻을 가지는 언어를 의미한다.
보통 어휘 목록은 Regular Expression으로, 구문구조는 Context-Free Language로 정의하는 편인데, 어휘 목록도 CFL로 정의할 수 있지만 구현의 복잡도 때문에 두 가지를 함께 사용해 언어를 구현한다.

CFG를 쉽게 표기하기 위해 Bankus-Naur Form을 사용한다.
BNF 표기를 보고 Derivate나 Parse를 수행하자.
Derivation은 문법으로부터 문자열을 생성하는 과정이고,
Parse는 Derivation의 역과정으로 문자열이 문법에 부합하는지 확인하는 과정이다.
각 과정을 트리로 표현할 수 있는데, 파싱 트리와 유도 트리는 방향만 다르고 나머지 부분은 동일하다.
하나의 문자열이 여러 방식으로 파싱될 수 있는 경우 deterministic하지 않은 경우로 하나의 문자열에 대해 여러 트리가 유도될 수 있다.
모호함을 줄이려면 유도 순서를 정해야 한다.
Left-Most, Right-Most 방식으로 좌측이나 우측을 우선으로 치환한다는 순서를 정한다.
파서는 유효한 문법 구조를 재구성할 때 어떤 순서로 Symbol을 전개했다고 가정하는 과정을 거치는데..
LL 파서는 left-most derivation을 시뮬레이션하듯 분석하고, LR 파서는 right-most derivation을 역순으로 시뮬레이션한다.
역순으로 시뮬레이션한다는 부분이 중요한데..
LR 파싱은 좌측부터 문자열을 읽지만, 우측부터 유도된 것 처럼 트리를 밑에서부터 조립한다.
그러니 LR 파싱으로 나오는 트리와 Right Most Derivation으로 나오는 트리는 같다.
즉.. 파서가 내부적으로 어떤 유도 순서를 따라가는지를 기준으로 LL/LR을 정의한다.
생각해보면.. 탑다운 파싱은 Derivation처럼 위에서 아래로 분석하는거랑 똑같은 것 같은데..
Derivation이랑 같은 건 아니고, 이 입력이 이런 Derivation을 만들 수 있는가? 를 검증하는 작업을 수행하니 파싱이라고 할 수 있다.
LL 파싱과 LR 파싱이 모호함을 줄이기 위해 등장한 방식으로, LL(k) LR(k) 로 lookahead 개수를 지정해 모호성을 더 줄일 수 있다.
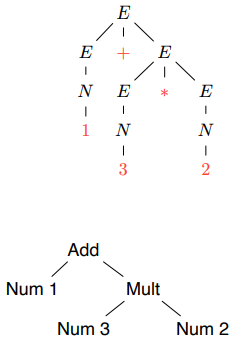
파싱을 통해 만들어지는건 AST이고, 그 과정에서 나오는 Parse Tree는 프로그램에 도움이 되지 않는다.
AST는 중간언어 (Intermediate Representation) 로 컴파일러나 인터프리터에서 쉽게 다룰 수 있는 자료구조이다.
(* lex 는 Regular Expression을 인식해서 token을 반환 *)
type token =
| IDENT of string
| NUMBER of string
| KW_LET
| KW_IN
| OP_EQ
| OP_PLUS
| OP_MINUS
type state =
| Q0 (* 초기 *)
| Q1 (* IDENT 읽는중 *)
| Q2 (* 숫자 읽는중 *)
| Q3 (* = 읽는중 *)
| Q4 (* + 읽는중 *)
| Q5 (* - 읽는중 *)
| Q6 (* 에러 *)
let transfer (s: state) (c: char) =
match s with
| Q0 ->
if 'a' <= c && c <= 'z' then Q1
else if '1' <= c && c <= '9' then Q2
else if c = '=' then Q3
else if c = '+' then Q4
else if c = '-' then Q5
else Q6
| Q1 ->
if ('a' <= c && c <= 'z' || 'A' <= c && c <= 'Z' || c = '_' || c = '\'') then Q1
else Q6
| Q2 ->
if '0' <= c && c <= '9' then Q2
else Q6
| Q3 | Q4 | Q5 -> Q6
| Q6 -> Q6
let rec rev (ls: char list) : char list =
match ls with
| [] -> []
| first :: left -> (rev left) @ [first]
let lex (str: string) : token =
let char_list = String.to_seq str |> List.of_seq in
let rec aux (s: state) (acc: char list) (left_list: char list) : token =
match left_list with
| [] ->
(match s with
| Q1 ->
let token_str = String.of_seq (List.to_seq (rev acc)) in
if token_str = "let" then KW_LET
else if token_str = "in" then KW_IN
else IDENT token_str
| Q2 ->
let token_str = String.of_seq (List.to_seq (rev acc)) in
NUMBER token_str
| Q3 -> OP_EQ
| Q4 -> OP_PLUS
| Q5 -> OP_MINUS
| _ -> failwith ("Lexing error: " ^ str))
| c :: left ->
let next_state = transfer s c in
if next_state = Q6 then failwith ("Lexing error: " ^ str)
else aux next_state (c:: acc) left
in
aux Q0 [] char_list
type expr =
| LetIn of string * expr * expr (* KW_LET IDENT OP_EQ e KW_IN e 매칭 *)
| Plus of expr * expr (* e OP_PLUS e *)
| Minus of expr * expr (* e OP_MINUS e *)
| Num of string (* NUMBER *)
| Id of string (* IDENT *)
type parse_stack_elem =
| T of token
| E of expr
let rec reduce (stack: parse_stack_elem list) (token_list: token list) (orgn_str: string) : parse_stack_elem list =
let rec reduce_impl (st: parse_stack_elem list) =
match st with
| E exp2 :: T KW_IN :: E exp1 :: T OP_EQ :: T (IDENT id) :: T KW_LET :: rest ->
(
match token_list with
| KW_IN :: _ | [] -> reduce_impl (E (LetIn (id, exp1, exp2)) :: rest)
| _ -> st
)
| E exp2 :: T OP_PLUS :: E exp1 :: rest ->
reduce_impl (E (Plus (exp1, exp2)) :: rest)
| E exp2 :: T OP_MINUS :: E exp1 :: rest ->
reduce_impl (E (Minus (exp1, exp2)) :: rest)
| T (NUMBER n) :: rest ->
reduce_impl (E (Num n) :: rest)
| T (IDENT id) :: rest ->
(
match token_list with
| OP_EQ :: _ -> st
| _ -> reduce_impl (E (Id id) :: rest)
)
| _ -> st
in
let reduced = reduce_impl stack in
if (reduced = stack) then stack else reduce reduced token_list orgn_str
let parse (str: string) : expr =
let word_list = String.split_on_char ' ' str in
let token_list = List.map lex word_list in
let rec parse_aux (stack: parse_stack_elem list) (tokens: token list) : expr =
match tokens with
| [] ->
let cur_stack = reduce stack [] str in
(
match cur_stack with
| [E e] -> e
| _ -> failwith ("Parsing error: " ^ str)
)
| t :: ts ->
let new_stack = reduce stack tokens str in
parse_aux (T t :: new_stack) ts
in
parse_aux [] token_list
문자열을 토큰으로 반환하는 Lexer와 문자열을 AST로 반환하는 Parser를 OCaml 언어로 구현한 예시이다.
Lexer는 패턴 매칭 말고 직접 Finite State Automata를 사용하는 방식으로 구현되어있다.
'Computer Science > Universial Programming Language' 카테고리의 다른 글
| [UPL] Recursion (0) | 2025.05.18 |
|---|---|
| [UPL] Conditional Branch (0) | 2025.05.15 |
| [UPL] 고차원 함수와 일차원 함수 (2) | 2025.04.18 |
| [UPL] Arithmetic Expression 정의 (1) | 2025.04.08 |
| [UPL] 함수형 언어 OCaml (0) | 2025.03.21 |
댓글
이 글 공유하기
다른 글
-
[UPL] Conditional Branch
[UPL] Conditional Branch
2025.05.15 -
[UPL] 고차원 함수와 일차원 함수
[UPL] 고차원 함수와 일차원 함수
2025.04.18 -
[UPL] Arithmetic Expression 정의
[UPL] Arithmetic Expression 정의
2025.04.08 -
[UPL] 함수형 언어 OCaml
[UPL] 함수형 언어 OCaml
2025.03.21