[Compiler Design] Machine Dependent Processing
이전까지는 IR을 어떻게 만드는지에 대해 다뤘으니, 이제 IR을 타겟 머신의 어셈블리 명령어로 매핑하고 명령어 순서를 재배치하는 작업에 대해 살펴보자.
즉, 컴파일러의 백엔드 부분에서는..
Instruction Selection / Instruction Scheduling / Register Allocation을 수행함.

Instruction Selection을 수행학시 위해 IR을 트리 구조로 표현한다.
좌측 트리는 e + c가 메모리에 있는 값을 나타내는 구조.
MEM / BINOP / PLUS / CONST 등의 노드로 트리를 표현한다.
MEM(e) - 주소 e에 있는 메모리의 값을 의미한다.
SEQ(s1, s2) - s1을 수행한 후 s2를 수행한다.
ESEQ(s, e) - s를 수행한 후 e의 결과를 반환한다. (s는 side effect 를 위해 수행)
여기서 s와 e는 프언개에서 다뤘듯.. Statement와 Expression을 의미한다.
같은 동작을 수행하지만 트리 모양이 다른 경우도 있다. (Equivalence)
트리의 모양을 정규화해서 추후 기계어 명령어와 매칭하기 좋은 형태로 만들 때 사용함.
Instruction Selection
두 가지 과정에 따라 진행된다.
1. 복잡한 트리 구조를 다루기 좋게 정리하는 Rewrite
2. 정리된 트리에 실제 기계어 명령어를 끼워 맞추는 Tiling
ESEQ (Execute Statement then Expression) 같은 노드가 트리 중간에 숨어있으면 기계어로 변환하는게 힘들다.
그러니 ESEQ를 트리의 가장 윗부분으로 끌어올려 코드를 순차적으로 만들어야 한다.

s 를 수행했을 때 e1에 들어갈 값이 바뀌고 결과가 달라지는 경우가 있다. (Side Effect)
이 때는 e1의 값을 임시 레지스터에 저장함.
트리를 깔끔하게 정리했으면, 이제 기계어 명령어에 맞는 타일을 트리에 붙여야 한다.

큰 트리 위에 여러 타일이 덮여있다. 여기서 각 타일은 기계어 명령어 하나와 1:1 대응됨.
최대한 큰 타일을 사용하는 편이 합리적이다.
큰 타일은 보통 한 방에 처리하는 명령어와 1:1 대응되고, 이러면 전체 명령어의 개수를 줄일 수 있음.
같은 트리여도 타일을 어떻게 붙이는지에 따라 결과가 좀 다름.
컴파일러의 최적화 수준, 타겟 머신의 명령어 set에 따라 달라질 수 있다.
트리에 타일을 다 붙였으면 아래에서부터 위로 타일을 하나씩 명령어로 변환한다.
Register Allocation
앞서 만든 코드는 아직 실제 레지스터를 다루고 있지 않고, 가상의 레지스터를 사용하고 있음.
이제 진짜 물리 레지스터에 끼워 넣어야 한다.
가상 레지스터에서는 모든 레지스터의 개수가 무한하다고 가정하는데, 실제 환경에서는 그렇지 않음.
자주 사용되는 변수를 레지스터에 넣고, 부족하면 어쩔 수 없이 메모리에 저장해야 함 (Spilling)
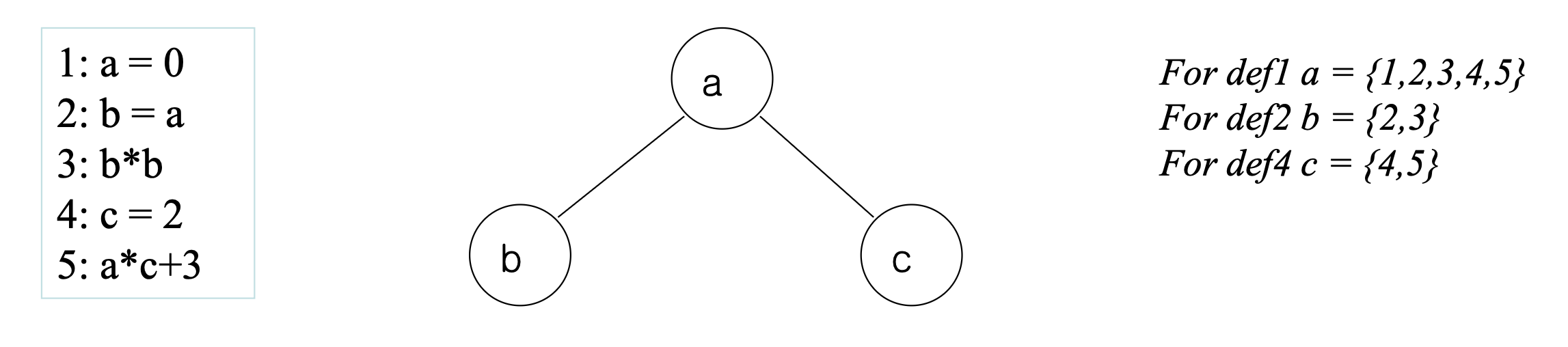

Interference Graph를 그려서 변수에 레지스터를 할당한다.
Interference : 두 변수가의 Live Range이 겹치는 것
여기서 Live Range는 변수가 정의된 시점부터 마지막으로 사용된 시점을 의미한다.
Node는 각 변수를 의미하고, 두 변수가 서로 간섭한다면 Edge로 연결한다.
변수 a의 Live Range : 1-5
변수 c의 Live Range : 4-5
4-5 구간에서 a와 c가 동시에 살아있으니 둘은 간섭한다. 그러니 서로 다른 레지스터랑 사용해야 함.
이걸 Graph Coloring 문제로 바꿔서 풀어보자.
a를 초록색으로 칠했으니 b와 c는 초록색을 사용할 수 없다.
b와 c가 서로 연결되어있지 않으면 둘 다 하늘색을 사용할 수 있다.
이러면 3개의 변수를 2개의 레지스터로 처리할 수 있다.
이론적으로 최소 몇 개의 레지스터를 사용해야 하는가? 는 NP-Complete 문제.
그러니 컴파일러는 Kempe's Algorithm이라는 휴리스틱을 사용해 레지스터를 할당한다.
Kempe's Algorithm
스택을 활용해 그래프를 단순화했다가 다시 복구하며 색칠하는 방식을 사용한다.
1. Simplify
그래프에서 Degree가 K보다 작은 노드를 찾는다. (K = 쓸 수 있는 레지스터 수)
이 노드를 그래프에서 잘라내고 스택에 넣는다.
여기서 찾은 노드는 나중에 그래프로 돌아왔을 때 이웃이 모든 색을 전부 쓰고 있어도 이웃 수가 K보다 작은 남는 색이 하나 이상 있음.
이 과정을 그래프의 모든 노드가 사라질 때 까지 반복한다.
2. Color
스택에서 노드를 하나씩 꺼내고, 꺼낸 노드를 그래프에 다시 복구시키며 이웃들이 사용하지 않은 색 하나를 칠한다.
애초에 이웃 수가 K보다 작으니까 무조건 칠할 색이 남아있음.
3. Spill
1번 과정에서 모든 노드의 이웃 수가 K보다 커서 지울 노드가 없으면? - 아무거나 골라서 스택에 넣는다.
어쩔 수 없음 -_-


3번 과정에서 넣은 노드들은 두 가지 방식으로 처리됨.
색칠하려고 보니 이웃들이 같은 색을 중복해서 사용해서 그대로 레지스터에 할당할 수 있는 경우. 이러면 참 좋은데
이웃이 색을 골고루 쓰고 있어서 레지스터 할당이 불가능 할 때가 있음. 이러면 해당 변수를 메모리로 쫓아낸다.
레지스터에 할당이 불가능하면 코드를 다시 작성해야 한다.
spill된 변수를 저장할 메모리 공간을 정하고, 해당 변수를 사용하는 명령어 전후에 LOAD / STORE 명령어를 추가한다.
Instruction Scheduling
명령어의 순서를 바꿔서 지연 시간을 줄이고 수행 속도를 높인다.
앞의 명령어가 끝날 때 까지 CPU가 일을 안하면 그만큼 자원이 낭비된다.
ADD는 금방 끝나는데, LOAD는 오래 걸릴 수 있다.
CPU는 Pipeline을 통해 여러 명령어를 동시에 처리할 수 있으니 LOAD가 진행되는 동안 ADD를 처리하면 효율적임.

스케쥴링 전에는 LOAD 전후에 그 값을 사용하는 MULT 명령어가 나온다.
LOAD는 오래 걸린다. MULT는 데이터가 도착 할 때 까지 기다려야함.
첫 번째 LOAD를 실행하고 바로 다음 LOAD 명령을 미리 던져놓는다.
이렇게 LOAD를 미리 다 깔아두고 데이터가 도착할 때 쯤 MULT를 수행하면 속도가 훨씬 빨라진다.
Instruction Scheduling도 사실 NP-hard 문제이다. 그래서 그리디 알고리즘인 List Scheduling 알고리즘을 사용한다.

1. Precedence Graph 작성
명령어 간 선후관계가 있을 수 있음.
누가 누구보다 먼저 실행되어야 하는지를 그래프로 표현한다.
2. Priority 결정
각 명령어에 점수를 매겨 Latency가 가장 긴 경로에 높은 우선순위를 할당한다.
3. Scheduling Loop
바로 실행할 수 있는 명령어들을 Ready Queue에 넣고, 우선순위가 가장 높은 요소를 꺼내서 스케쥴링한다.
모든 명령어가 배치될 때 까지 반복~
'Computer Science > Compiler Design' 카테고리의 다른 글
| [Compiler Design] Analysis and Optimization (0) | 2025.12.04 |
|---|---|
| [Compiler Design] Semantic Analysis (0) | 2025.11.25 |
| [Compiler Design] Run-Time Storage Management (0) | 2025.11.24 |
| [Compiler Design] Intermediate Representation (0) | 2025.11.24 |
| [Compiler Design] SDD / AST (0) | 2025.11.17 |
댓글
이 글 공유하기
다른 글
-
[Compiler Design] Analysis and Optimization
[Compiler Design] Analysis and Optimization
2025.12.04 -
[Compiler Design] Semantic Analysis
[Compiler Design] Semantic Analysis
2025.11.25 -
[Compiler Design] Run-Time Storage Management
[Compiler Design] Run-Time Storage Management
2025.11.24 -
[Compiler Design] Intermediate Representation
[Compiler Design] Intermediate Representation
2025.11.24