[ML] Dimensionality Reduction
차원이 늘어날수록 공간은 기하급수적으로 커진다. 데이터는 한정되어 있는데, 공간만 넓어지면 데이터 사이의 거리가 멀어진다.
텅 빈 고차원 공간을 제대로 설명하기 위해 더 많은 입력 데이터가 필요함. (Feature n개 == n차원)
Feature 수가 늘어날수록 Classifier의 성능이 올라갈 수 있음. 정보가 많아지니까~
하지만, Optimal Point를 지나면 오히려 성능이 급격히 떨어진다.
정답을 맞추는데 필요 없는 데이터가 섞이고, 같은 정보를 담은 변수가 여러 개 생기고, Overfitting이 발생하고 오버헤드가 커지기 때문.
모든 Feature가 독립적이라면, Feature가 많을수록 성능이 좋아야 한다.
그런데 현실의 데이터에서 모든 Feature가 독립적인건 절대 불가능하고, 데이터에 노이즈나 불필요한 정보도 포함되어있음.
그러니, Dimensionality Reduction이 필요하다.
전체 특징 중에서 더 작은 부분집합을 선택하자. 목표는 크기를 최대한 줄이고 성능을 최대한 끌어올리는 것.
Feature Selection
원래 있던 Feature 중에서 진짜 중요한거만 골라내는 작업. 두 가지 방식으로 진행된다.
1. Filter Approach
학습 알고리즘과는 무관하게 전처리 단계에서 Feature를 모두 골라내고 학습시킨다.
계산이 빠르고 단순하긴 한데, Optimal한 선택이 아닐 수 있음.
2. Wrapper Approach
실제로 학습 모델을 돌려보고, 피드백받고 집합을 수정한다.
모델 성능을 직접 확인하니까 정확도는 높다. 다만, 계속 학습시켜야돼서 계산 비용이 비싸고 시간도 오래 걸림.
브루트포스 때려버리는것도 방법인데, 이러면 컴퓨터가 너무 힘들어한다. 타협안이 필요함. (Heuristics)
Forward Search - 0부터 시작해서 하나 추가하고 테스트. 가장 좋은거 fix. 이 과정을 반복
Backword Elimination - 일단 다 들고 시작해서 하나씩 빼면서 제거. Forward Search랑 반대 방식임.
Stepwise Search - 두 방식을 섞어서 사용한다. 가장 좋은거 하나 추가하고 중요도 떨어진거 있으면 제거함. (페널티 추가)
Search 말고 학습 과정에서 Feature를 제거하는 방식도 있음.
LASSO 방식은 Loss Function에서 가중치 절댓값의 합을 더해서 최소화하는데, 이러면 중요하지 않은 Feature의 가중치가 0이 된다.
가중치가 0이면 해당 Feature가 모델에서 제거됨을 의미함.
Forward Search와 Backword Elimination 방식은 탐색 순서가 정해져 있어 Local Optimum에 도달하는 경우가 많음.
그래서 Genetic Algorithm을 사용한다. Global Optimum에 가까운 Solution을 찾는게 목표.
말 그대로 자연 선택과 진화의 과정을..... 컴퓨터로 구현해서 최적해를 찾는 알고리즘임.
Feature Subset을 생물학 용어에 대입해서 이해해보자.
Individual - Feature Subset - 해답 후보
Gene - Feature - 개별 변수
Chromosome - Binary String - 선택된 특징 리스트
Fitness - Accuracy - 이 조합이 얼마나 유용한지를 숫자로 표현
Population - Feature 조합 후보 - 특징 조합
5개의 Feature를 가지고 있다면, 1 0 1 1 0 은 X1 X3 X4만 선택하고 나머지는 버린 조합을 의미한다. 조합은 하나의 객체임.
이 조합으로 모델을 학습시킬 때 정확도가 92%면, 이 객체의 Fitness는 0.92
Fitness를 계산할 때 정확도가 비슷하면 Feature 개수가 적은 조합에 더 높은 점수를 주기도 함. (AIC / BIC 사용)
AIC - 최소한의 변수로 최대한의 성능을 내는 모델을 찾을 때 사용함.
과적합 방지를 위해 AIC 값이 작을수록 좋음. 성능이 비슷하면 Feature가 적은 간단한 모델을 선택할 때 씀.
1. initialization
무작위로 Feature Subset을 여러개 생성해서 Population을 만든다.
2. Evaluation
집단 내의 모든 Feature Subset을 하나씩 꺼내서 학습시키고 정확도를 측정함.
모델별로 Fitness 를 구한다.
3. Selection
적합도가 높은 객체들을 다음 세대를 만드는 Parents로 선택한다.
정확도가 95%인 조합은 90%인 조합보다 부모가 될 확률이 더 높음.
4. Crossover
선택된 Parent 두 개를 골라서 정보를 섞어 새로운 자손을 만든다.
좋은거를 합쳐서 부모보다 더 좋은 Feature 조합을 만드는게 목표.
5. Mutation
Crossover로 생성된 자손의 Feature 중 일부를 무작위로 뒤집는다. 너무 자주 일어나면 안되니 매우 낮은 확률로 변이를 발생시킴.
Local Optimum에 고착되는걸 방지한다. 긴장감을 불러일으키는..
6. Termination
2 - 5 단계까지가 하나의 Generation. 이 과정을 계속~ 반복한다.
미리 정한 Generation 수에 도달하거나 성능이 더 이상 개선되지 않을 때 멈춘다.
즉, 특징 조합 랜덤돌려서 만들고 성능 좋은거만 살게함.
그 조합끼리 장점 섞고.. 가끔 돌연변이로 긴장감을 주는..
최종적으로는 여러 세대를 거치면서 가장 완벽한 Feature 조합을 찾아내는 알고리즘이다.
하.. 과탐으로 생명 했으면 좀 편하게 했을텐데.
Feature Extraction
Feature Selection은 있는 거 중에서 고르는 작업이고, Feature Extraction은 데이터를 조작해서 새로운 Feature를 창조하는 작업임.
기존의 Feature를 적당히 섞어서.. 0.5x1 + 0.5x2 이런식으로.. 데이터를 가장 잘 설명하는 새로운 축을 찾는게 목표.

x1과 x2 대신 빨간 선으로 데이터를 바라보고 있음.
Principal Component Analysis (PCA) 는 데이터의 특징을 가장 잘 살리는 방향을 찾는 것.
복잡하고 변수가 많은 고차원에서, 데이터를 잘 회전시켜서 가장 넓게 퍼져 보이는 방향인 PC1을 찾는다.
그 방향을 기준으로 데이터를 다시 배치해 차원을 줄이면서 Feature는 최대한 남김.
근데 저걸 어떻게 찾음?
Variance를 제대로 이해해야 함.
데이터가 한 곳에 뭉쳐있으면 (Variance가 낮으면) 누가 누구인지 구별하기 힘들다.
데이터가 넓게 펼쳐져 있으면 (Variance가 크면) 데이터 간의 차이를 명확하게 알 수 있다.
데이터를 선 위로 Projection 했을 때, 그림자가 가장 길게 늘어지는 축을 찾는게 목표.
즉, 새로운 축 위로 데이터를 Projection 했을 때 Variance가 커야 한다.
PCA는 데이터를 회전시키며 관찰해야 하니, 현재 어떤 모양과 어떤 방향으로 퍼져있는지에 대한 설계도가 필요함.
Covariance Matrix (S) 를 설계도로 사용한다.

두 변수가 함께 어떤 방향으로 얼마나 움직이는지 알아야 함.
행렬 S를 조작하면서 최적의 w를 찾는다.
축 w위로 데이터를 Projection 했을 때의 분산은 w^TSw 로 표현됨.
여기서 w를 10배 길게 늘린 벡터를 쓰면 분산은 100개 늘어나게 됨. 방향만 찾고싶은거니 w의 길이를 1로 고정하자.
즉, PCA는 길이가 1인 벡터인 w 중에서 Covariance Matrix aS와 곱했을 때의 분산을 최대로 만드는 벡터 w를 찾는 문제로 바뀜.
저거를 찾는건 미분으로 안된다. 여기서 또 라그랑주 승수법을 사용한다.
식정리 어떻게 잘 하면 Sw = λw 이렇게 나옴. 다 까먹었지만 선형대수에서 Eigenvalue-Eigenvector 수식이 이렇게 생김.
식을 잘 풀어주면 여러 쌍의 w와 λ가 나온다.
w는 PC들의 방향을 의미하고, λ는 분산의 크기를 의미한다. (w로 Projection했을 때의 분산이 λ와 동일함)
왜? 그냥 계산했더니 λ가 분산의 크기였음.
w가 PC의 방향인거는 Eigenvector의 정의 그 자체.
역시 다 까먹었지만 선형대수에서 다뤘듯 특정 벡터는 S를 곱해도 방향이 안 바뀌고 길이만 λ배 늘어나는데, 공분산 행렬 S에서 방향이 안 바뀌는 이 축이 데이터가 퍼져 있는 Principal Component가 된다.
PC 끼리는 서로 수직임.
즉, PC1이 설명한 정보와 PC2가 설명한 정보는 절대로 겹치지 않고 서로 독립적이다.
계산으로 얻은 λ가 큰 순서대로 PC1 PC2.. 오름차순으로 배치해줌.
PC를 만들 때는 w만 필요하긴 하다. 그런데, λ를 구하면 어떤 w를 선택하고 어떤 w를 버릴지 결정할 수 있음.
정보를 가장 많이 담고 있는 w를 골라서 차원을 축소해야 하는데, 어떤걸 골라낼지에 대한 기준으로 λ를 사용함.
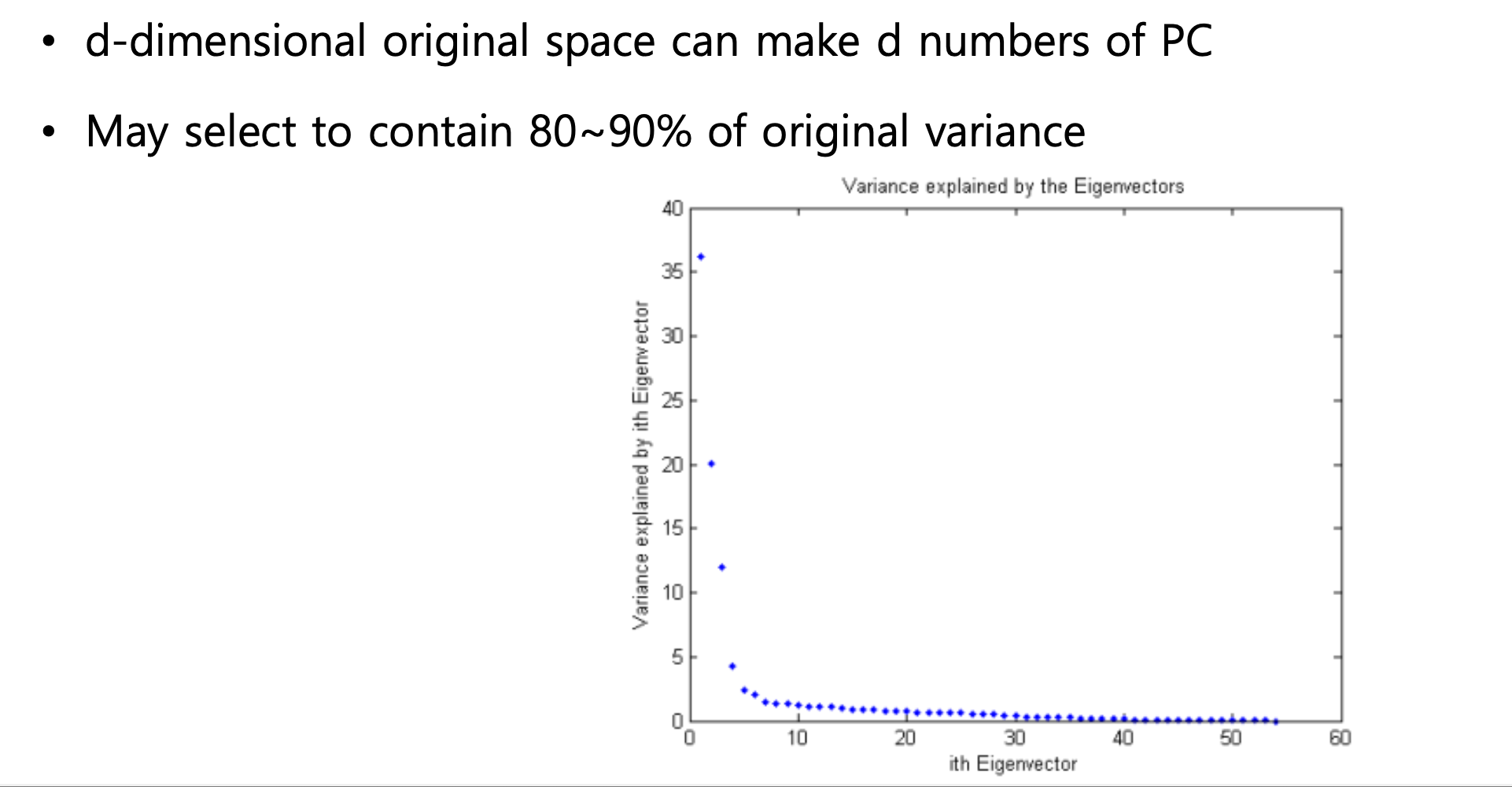
몇 개의 PC를 선택할지도 정해야 함.
λ로 PC의 순위를 매겼는데, 여기서 몇 개를 선택해야 할까?
웬만하면 총 분산의 80% ~ 95%를 설명하는 PC까지만 남긴다.
그래프를 보면 값이 급격하게 떨어지는 구간이 있는데, 그 지점까지만 선택하는 편.

PC1을 실제로 사용해서 Projection 할 때는 내적으로 계산한다.
w를 찾고 원본 데이터를 새로운 Low Dimension 좌표계로 변환해야 하는데, 이 때 내적을 씀. (Dot Product == Projection)
대수 관점에서는 내적이고 기하 관점에서는 Projection.
'Computer Science > Machine Learning' 카테고리의 다른 글
| [ML] Kernel Method (0) | 2025.12.07 |
|---|---|
| [ML] Deep Neural Networks (0) | 2025.12.06 |
| [ML] Neural Networks (0) | 2025.12.06 |
| [ML] Ensemble Method (0) | 2025.12.05 |
| [ML] Decision Tree (0) | 2025.10.18 |
댓글
이 글 공유하기
다른 글
-
[ML] Kernel Method
[ML] Kernel Method
2025.12.07 -
[ML] Deep Neural Networks
[ML] Deep Neural Networks
2025.12.06 -
[ML] Neural Networks
[ML] Neural Networks
2025.12.06 -
[ML] Ensemble Method
[ML] Ensemble Method
2025.12.05