Deep Learning - Backpropagation

단일 층으로 구성돼있는 Neural Network에는 Gradient Descent를 사용하는게 합리적이다.
Backpropagation은 여러 층으로 구성된 상황에서 오류가 최소가 되는 가중치 w를 결정하는 방법이다.
기본적인 틀은 Gradient Descent를 따른다.
먼저 Computation Graphs와 Loss function을 정의한다.
Loss 함수는 평가지표를 위해 정의한다. (Cost 함수로도 불림)
입력값과 weight(가중치)를 통해 출력값을 도출한다. (FORWARD DIRECTION)
이 때 처음 가중치는 무작위로 정한다. (Gradient Descent와 비슷함)
다음으로 출력값과 정답값을 통해 Loss를 계산하고.
Loss를 통해 가중치를 업데이트한다. (BACKWARD DIRECTION)
여기서 가중치 업데이트는 Gradient Descent 알고리즘 방법을 따른다.
위의 과정을 반복해서 새로운 Test값에 대해서도 Loss를 줄이는 방향으로 학습을 진행한다.

잠시 Gradient Descent를 리마인드하고 가자.
기울기의 절댓값이 작아지는 방향으로 W를 이동시킨다.

앞에서 언급했던 Computational Graph이다. 파란박스의 값(A,B,P,Q)은 입력값으로 들어오는 값이나 계산을 통해 얻어지는 값이다.
W1 W2 W3 값은 우리가 찾아야 하는 값이다. 일단은 Computational Graph가 이런식으로 생겼구나~ 정도만 파악하자.
이 다음은 Loss 함수를 정의한다.
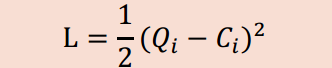
여기서 Q는 출력에 대한 결과값이고 C는 결과값에 대한 정답 레이블로 생각할 수 있다.
기본적으로 Q값과 C값을 매칭시키고 이에 맞춰 W를 갱신하는게 목표이다.
Loss함수에 1/2을 곱하는 이유는 Gradient Descent때와 마찬가지로 어차피 Loss함수는 미분될 운명이기 때문에 계산의 편의를 위해서이다. (컴퓨터에게 명령할 때 1/2을 붙이는 것과 붙이지 않는 것이 의미있는 차이를 가져온다.)
다음으로 FORWARD 방향으로 계산을 진행하자.
첫번째 데이터에 대해 Q는 8이고 정답 레이블은 5이다.
이를 바탕으로 Loss 함수를 계산하면 9/2가 나오고, 이제 가중치를 업데이트하자.
Backpropagation을 하는 목적은 Gradient Descent 방법처럼 만들어서 모르는 가중치인 W를 이상적으로 만들어주기 위해서이다. 이를 위해 Loss함수와 가중치 W에 대한 편미분 (partial derivation)이 필요한데, 위의 상황에서 Q를 P에 대한 식으로 작성하고 Loss 함수 식에 넣어서 계산하게 되면 함수의 차수가 점점 늘어나게 되고 미분이 힘들어진다.
(사람이 풀 수 없고 컴퓨터가 좋아하지 않은 비선형식이 된다.)
여기서 Backpropagation이 사용된다.
지금 알고 있는 건 Loss함수 / P에 대한 관계식 / Q에 대한 관계식이다.
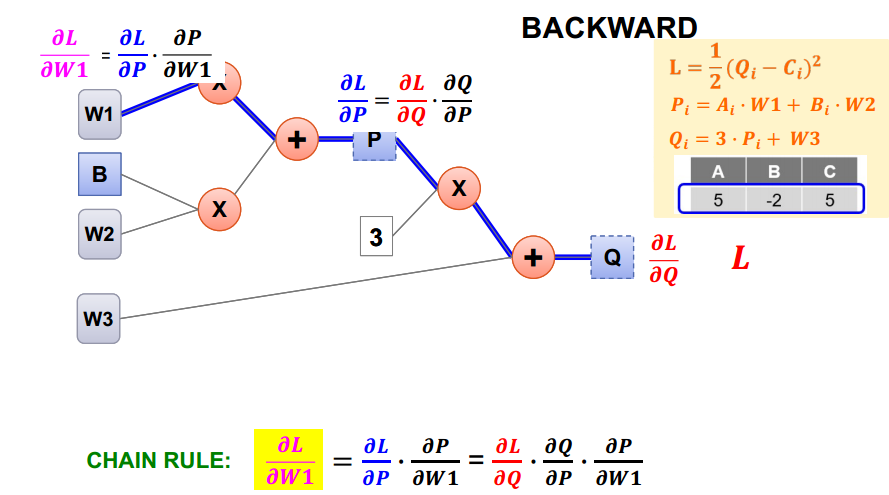
위처럼 Q에서부터 미분식을 작성해서 W1까지 향한다.
라이프니츠식으로 미분을 표기했고, 아래 CHAIN RULE을 보면 알수 있듯, 원하는 값을 여러 가지로 쪼개서 쉽게 구할 수 있게 됐다.
고등 수학 과정에서 합성함수 미분을 증명하는 부분과 유사하게 진행된다.
애초에 Q를 P에 대한 합성함수로 보고 미분한다면 같은 결과가 나올 것이다.
W1은 물론 W2와 W3에 대해서도 이 방법으로 L을 W에 대해 미분한 결과를 얻을 수 있고, 이 결과값을 통해 Gradient Descent 방법을 적용시킨다.
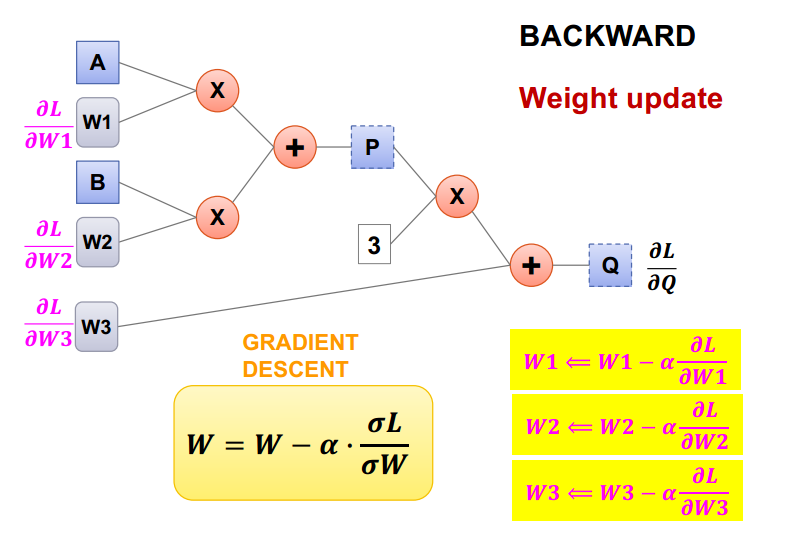
Gradient Descent 방법으로 가중치를 갱신해준다.
Loss함수값이 충분히 작아질 때 까지 반복한다.

지금까지의 내용을 정리해보자.
여러 층으로 구성된 Neural Network에서 가중치를 갱신하는 방법을 backpropagation이라고 한다.
Gradient Descent를 수행하는 과정에서 미분값을 알지 못하는 문제를 합성함수 미분 방식을 이용한 backpropagation을 통해 해결한다.

Loss 값이 0이 될 때 까지 하는건 좋지 않다. (지난시간에 배운 Overfitting 문제를 생각하자.)
아 그래 backpropagation이 이런거구나...그런데 왜 backpropagation을 하려 했었지???
Multi-Layer Perceptron(Neural Network) 에서 XOR을 간단하게 처리하기 위해서이다.

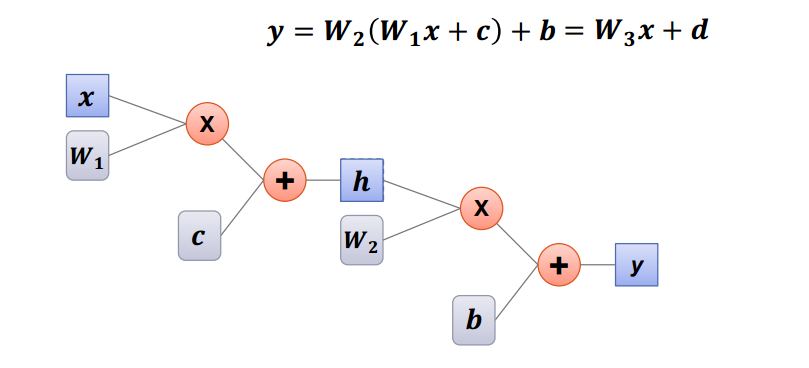
XOR 구현을 위해 Linear Model을 여러 층으로 쌓아주자.
하지만 Linear Model을 여러 개 겹친다고 해서 차원이 늘어나지는 않는다.
Linear Model만으로는 고차원인 XOR을 구현할 수 없다.
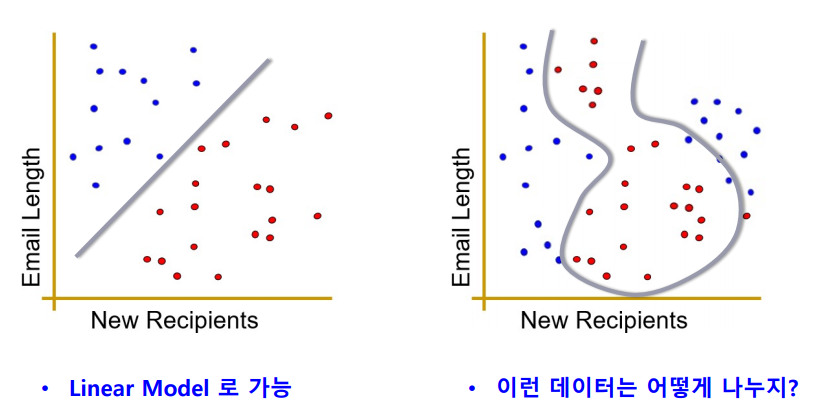
스팸 메일을 구분하는 예시를 생각해보자.
Linear Model로는 왼쪽의 경우는 잘 구분할 수 있지만, 오른쪽의 경우는 구분할 수 없다.
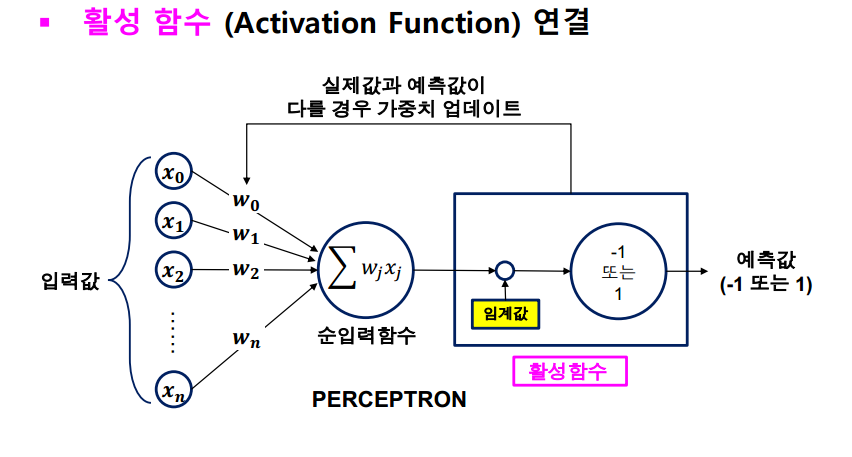
그래서 활성함수가 도입됐다. (활성함수는 nonlinear)
그러면?
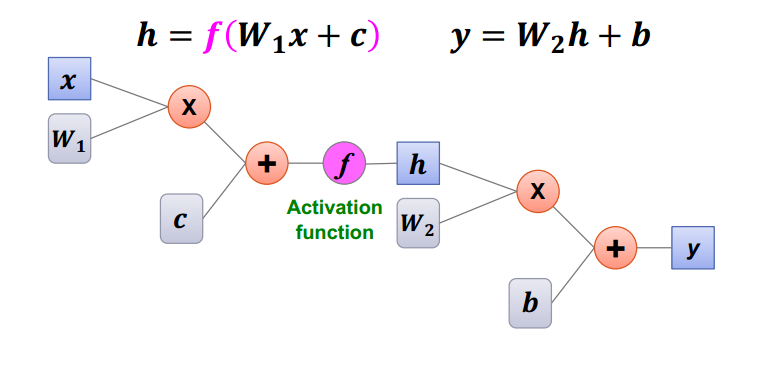
활성함수로 두 가지 Linear Model을 연결시키자.
이런 식으로 만들어진 MULTI-LAYER PERCEPTRON (MLP)은 어떤 모양의 데이터도 분류할 수 있다.
이 MLP를 간소화해서 표현하면
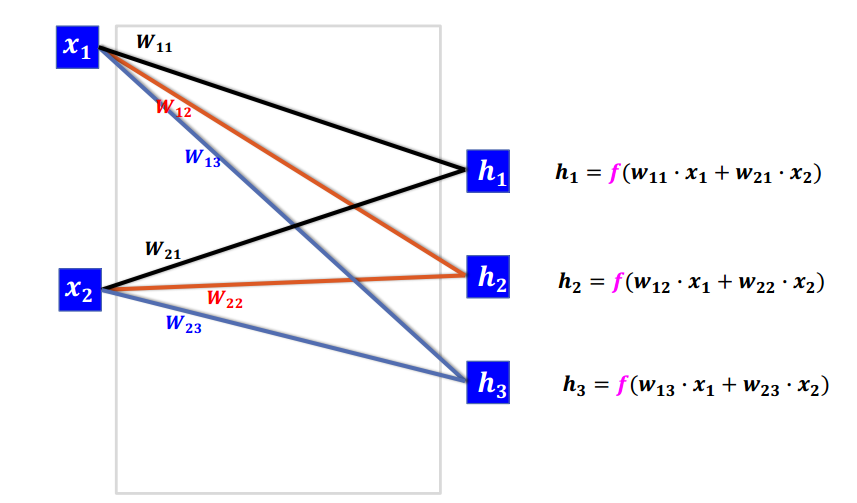
위와 같이 표현할 수 있다. (W와 계산기호 생략)
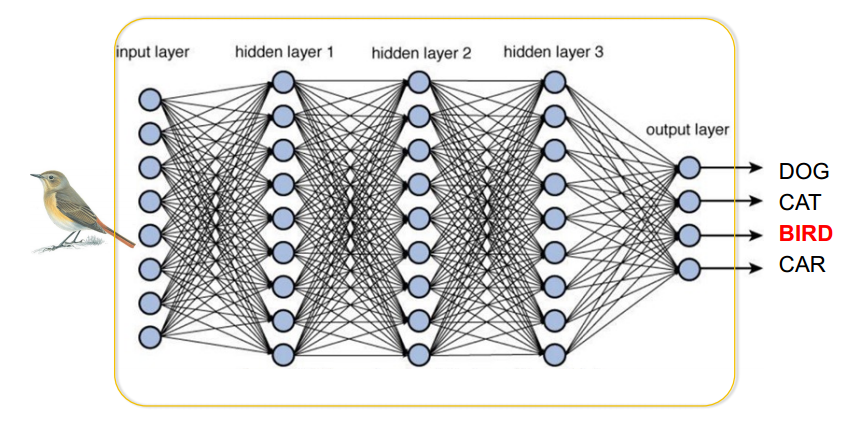
지난시간에 봤던 그림을 다시 한 번 보자.
아는 만큼 보이지 않는가?
'Machine Learning > AI Introduction' 카테고리의 다른 글
| Deep Learning (4) (0) | 2021.12.03 |
|---|---|
| Deep Learning (3) (0) | 2021.11.18 |
| Deep Learning (2) (0) | 2021.11.14 |
| Deep Learning (1) (0) | 2021.11.14 |
| Machine Leaning - Overfitting (0) | 2021.10.24 |
댓글
이 글 공유하기
다른 글
-
Deep Learning (4)
Deep Learning (4)
2021.12.03 -
Deep Learning (3)
Deep Learning (3)
2021.11.18 -
Deep Learning (2)
Deep Learning (2)
2021.11.14 -
Deep Learning (1)
Deep Learning (1)
2021.11.14