[컴퓨터 구조] 데이터의 표현
https://13months.tistory.com/477
컴퓨터가 이진수 체계를 사용하는 이유에 대해 살펴봤다.
컴퓨터가 사용하는 데이터의 표현 방식에 대해 간단히 알아보자.
숫자는 이진수로 표현하고, 문자나 기호는 7비트의 ASCII코드를 사용해서 표현한다.
뺄셈 연산과 논리 연산 시 보수 개념이 사용된다.
컴퓨터는 이진수 체계를 사용하니, 1의 보수와 2의 보수 중 하나를 선택해서 사용하면 된다.
r진법에서 (r-1)의 보수는 (r^n - 1) - N 으로 정의된다. (n은 자릿수, N은 r진법의 수)
r진법에서 r의 보수는 (r^n) - N 으로 정의된다. (n은 자릿수, N은 r진법의 수)
보수에 보수를 취하면 원래 수로 돌아온다.
이진수에서 MSB(제일 왼쪽 비트)를 부호 비트로 사용해 양수와 음수를 표현한다.
MSB가 0이면 양수, 1이면 음수를 의미한다. (관례로 생각하자)
컴퓨터에서 1의 보수를 사용하게 되면 0에 대해 음수 0과 양수 0이 가지는 문제점이 발생한다.
따라서 2의 보수를 사용해 뺄셈 연산과 논리 연산을 수행하고, 음수를 더한다는 개념으로 접근한다.
덕분에 동일한 hardware circuit으로 뺄셈과 덧셈을 모두 구현할 수 있게 됐다.
컴퓨터의 산술 연산 로직이 사람의 로직과 다르다는 점에 주의하자.
컴퓨터에서는 레지스터의 길이가 한정돼있기 때문에 오버플로우가 발생할 수 있다.
두 수가 같은 부호를 가지며, 두 수에 대해 가산 연산을 수행하면 오버플로우가 발생할 수 있다.
덧셈 결과 최상위 두 비트에서 발생한 캐리를 XOR시켰을 때 1을 얻는다면 오버플로우가 발생했다고 할 수 있다. (두 캐리가 다를 때)
소수를 표현할 때는 소수점을 가장 오른쪽 혹은 왼쪽에 고정시켜서 표현하는 Fixed-point 방식을 사용하거나 Floating-point 방식을 사용한다. (부동 소숫점 : https://13months.tistory.com/487)
이진 정보 전송 시 에러가 발생함을 방지하기 위해 패리티 비트를 사용한다.
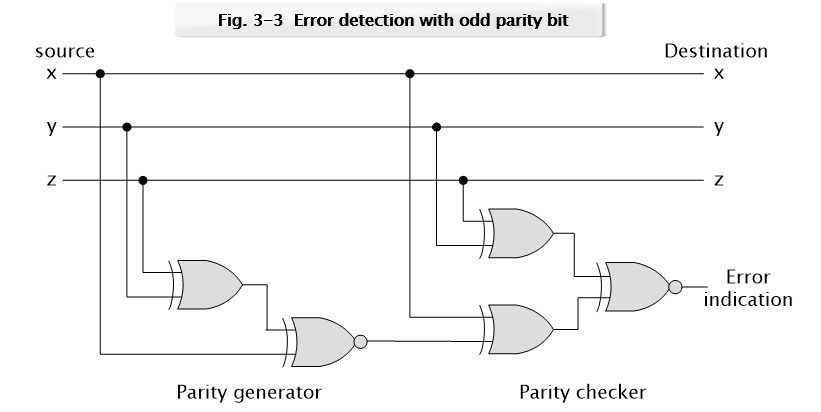
좌측에 패리티 발생기가 있고 우측에 패리티 검사기가 있다.
검사기의 출력과 발생기의 출력이 같으면 (Error indication 값이 0이면) 에러가 없다고 할 수 있다.
대부분의 에러는 single 에러이고 잘 발생하지도 않는다.
에러가 2번 발생하는 경우는 정말 드물고, 짝수 개의 비트에서 발생하는 에러는 고려하지 않기로 한다.
'Computer Science > Computer Architecture' 카테고리의 다른 글
| [컴퓨터 구조] 기본 컴퓨터 프로그래밍 (0) | 2022.10.09 |
|---|---|
| [컴퓨터 구조] 기본 컴퓨터의 구조와 설계 (2) | 2022.10.04 |
| [컴퓨터 구조] 레지스터와 마이크로 연산 (0) | 2022.10.02 |
댓글
이 글 공유하기
다른 글
-
[컴퓨터 구조] 기본 컴퓨터 프로그래밍
[컴퓨터 구조] 기본 컴퓨터 프로그래밍
2022.10.09 -
[컴퓨터 구조] 기본 컴퓨터의 구조와 설계
[컴퓨터 구조] 기본 컴퓨터의 구조와 설계
2022.10.04 -
[컴퓨터 구조] 레지스터와 마이크로 연산
[컴퓨터 구조] 레지스터와 마이크로 연산
2022.10.02