Machine Learning - Supervised Learning (4)
Supervised Learning의 여러 가지 알고리즘들에 대해 살펴보자.
1. Naïve Bayesian Classifier
2. Decision Tree
3. K-Nearest Neighbors
4. Linear Models
5. Support Vector Machine (SVM)
6. Multi Layer Perceptron(MLP)
4. Linear Models
선형 모델.
Classification
Regression
(Regression을 먼저 공부하고 Classification을 공부한다.)
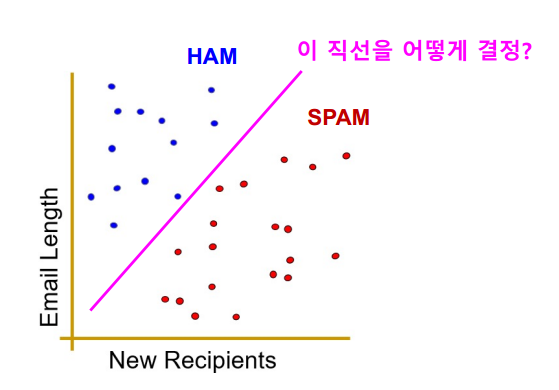
Decision Tree 알고리즘에서는 Boundary를 나눌 때 축 상으로 (바둑판처럼) 나눌 수 밖에 없지만, 선형 모델에서는 직선으로 분류할 수 있다.
y = ax +b
Linear Regression
공부한 시간에 따라서 시험에서 몇 점을 받을 수 있을까? 를 예시로 Linear Regression을 살펴보자.

위의 학습 데이터를 그래프로 표현해 선형으로 표현할 수 있다면 Linear Regression으로 문제를 해결할 수 있다.
그러니 데이터가 선형 모델을 따를 수도 있고 다른 모델을 따를 수도 있지만, 선형 모델을 따른다고 가정하고 풀자.
결과를 추론할 때 추론의 Hypothesis를 따 와서 f(x) 대신 H(x)를 사용하기도 한다.
H(x) = Wx + b
이 모델에서 W와 b를 찾아가는 것을 학습한다 라고 표현한다.
즉, 어떤 데이터를 그래프로 표현했을 때 그 데이터들을 가장 잘 표현하는, 에러를 최소로 하는 W와 b를 찾는 것이 목표이다.
그러기 위해서 평가지표를 정의하는데, 이 평가지표가 최소가 되도록 특정한 매개변수(W,b)를 튜닝한다.
Cost Function. Loss Function, 오류 함수 라고도 불린다.
위와 같은 평가지표가 있다.
위의 함숫값을 최대한 작게 하는것이 목표이다.
H(x) - y : 각각의 점들이 의미하는 것이 y이고, Vector Line이 의미하는건 H(x)이다.
이 사이의 거리가 작을수록 좋다.
하지만, 이 식으로는 완벽하게 표현할 수 없다.
만약에 H(x) 와 y의 차이가 +1 +1 -1 -1 이렇게 있다고 하면, 오류를 잡아낼 수 없다.
그래서 (H(x)-y)^2 수식을 사용한다.
절댓값 대신 제곱을 사용하는데, 절댓값을 씌우게 되면 미분 불가능한 점이 생길 수 있기 때문이다.
위의 수식으로 전체 Data Set에 대한 오류 평균을 구한다.
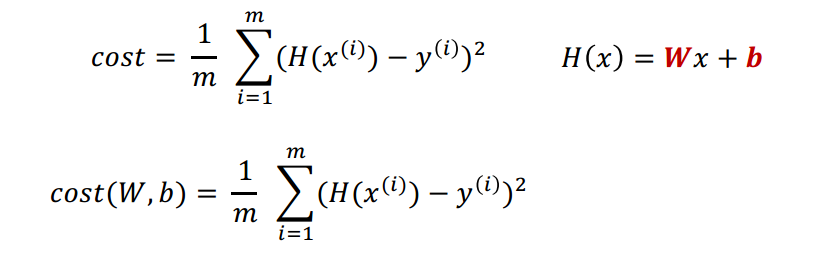
코스트를 정의할 때는 위의 수식과 같이 정의한다.
여기서 Linear Regression의 목표를 다시 한 번 상기하면,
Cost(오류)가 최소가 되는 W와 b를 찾는 것이 문제이고 Learning이다.
그냥 이차원 함수를 미분때려서 일차원으로 바꾸고 W,b 구하면 되는거아닌가?? 라고 생각할 수 있지만, 엄청나게 복잡한, data point도 많고 차원도 커질 때는 도함수로 한 번에 구하는게 힘들다. 그리고, 간단한 문제를 넘어서 이런 복잡한 문제까지 일관적으로 풀어낼 수 있는 해결책을 찾는게 목적이다.
이런 문제를 해결하기 위해 Gradient Descent가 도입됐다.
한 이차함수를 예를 들면
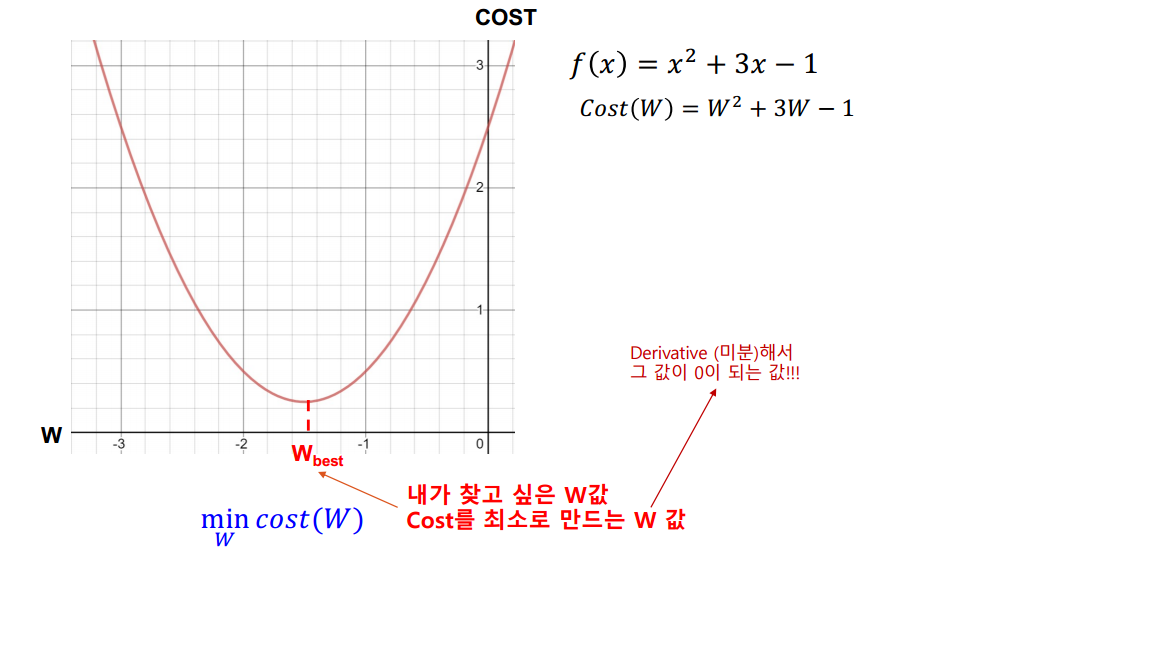
이차함수를 Cost(W)로 바꾸고 생각해보자.
Cost를 최소로 만드는 W의 값은 곡선의 기울기가 0이 될 때 이다.
물론, 복잡한 데이터가 주어진 상황에서는 이렇게 시각화하는것도 힘들지만, 예시를 위해 이차함수를 생각하자.
GRADIENT DESCENT
Gradient : 기울기
Descent : 하강
모르는 W의 값을 추정하는 방법이다.
Cost함수가 최소값이 되도록 W를 점진적으로 찾아주는 방법이다.
1. W를 임의의 값으로 초기화한다.
2. Cost함수의 기울기의 절댓값이 작아지는 쪽으로 W를 이동시킨다.
기울기를 빼는 방향으로 W를 이동시킨다.
즉, 도함수의 값이 양수이면 W의 값을 왼쪽으로 이동시킨다. (W의 값을 줄이는 방향으로)
도함수의 값이 음수이면 W의 값을 오른쪽으로 이동시킨다. (W의 값을 늘리는 방향)
도함수의 값이 0이라면 이동하지 않는다.
3. 반복하다 보면 Cost가 최소가 되는 W를 찾을 수 있다.
즉, W의 값은 도함수의 값이 0이 되면 반복을 멈춘다.
이제 Gradient Descent 방법을 이용해 Linear Model에서 W의 값을 추정해 보자.

최적의 W를 찾는 목적에 대해서 2로 나눠주는 건 영향을 미치지 않으므로 2로 나눠서 식을 다시 정의했다.
(이차함수 형태에서 2를 곱하든 나누든.. 도함수가 0 이 되는 점은 변하지 않는다.)
2로 나눠준 이유는, 제곱을 미분할 시 2를 앞에 곱하게 되는데 그걸 깔끔하게 표현하기 위해서이다.
그런데, 차원이 커지고 그에 따라 변수가 많아진다면 여러 가지 변수에 대해 미분을 수행해야 한다.
이때 편미분을 사용한다.
(다중 변수의 함수를 한 변수에 대해 미분할 경우 나머지 변수는 상수인 것 처럼 취급.)
정리해보면

즉 위의 식은 직관적으로 이해한 Gradient Descent를 수학적으로 구현한 결과라고 볼 수 있다.
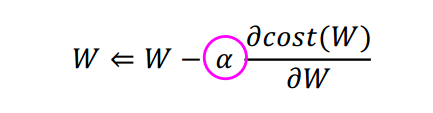
Gradient Descent로 문제를 해결할 때, W를 업데이트 하는 과정에서 학습률을 의미하는 알파를 도입한다.
위의 수식에서 알파는 W 값을 얼마나 많이 이동시킬지를 의미한다.
이차함수에서 W값을 한 번에 많이 이동시킬수록 초기 W값을 원하는 W값에서 멀리 설정했을 때는 유용하겠지만, 가깝게 설정했을 때는 유용하지 않을 수 있다.
알파를 어떻게 설정해야 하는지는 문제 상황에 맞는 솔루션이 이미 구비돼 있기 때문에 걱정할 필요는 없다.
'Machine Learning > AI Introduction' 카테고리의 다른 글
| Machine Learning - Unsupervised Learning (0) | 2021.10.17 |
|---|---|
| Machine Learning - Supervised Learning (5) (0) | 2021.10.17 |
| Machine Learning - Supervised Learning (3) (0) | 2021.10.17 |
| Machine Learning - Supervised Learning (2) (0) | 2021.10.17 |
| Machine Learning - Supervised Learning (1) (0) | 2021.10.17 |
댓글
이 글 공유하기
다른 글
-
Machine Learning - Unsupervised Learning
Machine Learning - Unsupervised Learning
2021.10.17 -
Machine Learning - Supervised Learning (5)
Machine Learning - Supervised Learning (5)
2021.10.17 -
Machine Learning - Supervised Learning (3)
Machine Learning - Supervised Learning (3)
2021.10.17 -
Machine Learning - Supervised Learning (2)
Machine Learning - Supervised Learning (2)
2021.10.17