[UPL] Arithmetic Expression 정의
Syntax와 Semantics를 정의해 간단한 언어인 Arithmetic Expression을 정의해보자.
AE는 정수 사이의 덧셈과 뺄셈으로 구성된다.

Concrete Syntax

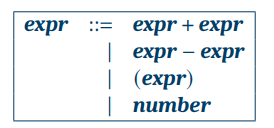
BNF 를 사용해서 정의한다.
개발자가 직접 작성하는 코드의 구조와 모양으로, 실제로 코드에서 보게 되는 문자 단위의 문법을 의미한다.
파싱에서 중요한 역할을 수행하고, 언어의 문법을 정의할 때 첫 단계로 사용된다.
Abstract Syntax
프로그램을 나타내는 트리 형태의 구문구조이다.
프로그램은 여러 개의 구문으로 구성되고.. 각 구문은 또 세부 구문으로 구성된다.
파서가 이미 파싱해서 AST를 줬고.. 이 AST는 컴파일러나 인터프리터가 사용한다.
즉, Concrete Syntax를 파싱하면 Parse Tree가 나오고.. 이걸 바탕으로 또 Abstract Syntax가 나오고.. Abstract Syntax를 트리로 표현한게 AST.
재귀적 구조 덕분에 프로그램은 트리 형태로 표현하기 좋다.
프로그래밍 언어의 문법은 재귀적인 경우가 많고, 트리는 재귀적인 구조를 자연스럽게 표현할 수 있고..
트리 자료구조는 순회도 쉽고 분석과 변환도 체계적으로 수행할 수 있어 유용하다.

Abstract Syntax는 Concrete Syntax가 어떻게 구성되어있는지 전혀 알 필요가 없다.
실제 코드에서 사용되는 괄호, 세미콜론 같은 문법적 디테일을 제거하고, 문법의 핵심 구성 요소와 그 의미만 Abstract Syntax Tree로 표현해 컴파일러와 인터프리터의 중간 언어로 활용한다.

AST 가 만들어지기는 부분을 기점으로 Frontend와 Backend가 나뉘니까..
AST는 핵심에만 집중해 Backend가 읽어서 처리하기 좋은 형태로 구성한다고 생각하자.
type expr =
| Num of int
| Add of expr * expr
| Sub of expr * expr

정의한 AE의 Abstract Syntax로 AE 프로그램을 AST로 표현하면 위와 같은 트리가 만들어진다.
여기서 연산의 우선순위를 정하기 위한 괄호는 불필요한 문법적 요소인데..
괄호는 개발자나 파서가 우선순위를 명확하게 이해하기 위해 사용하는 장식으로, AST는 노드의 계층과 위치로 연산의 우선순위가 자동으로 표현되기에 괄호를 트리에 표현하지 않아도 된다.

Abstract Syntax는 주로 축약된 코드 형태로 기술된다.
위의 그림에서 +와 -는 수학 연산자가 아니고, Expr 도메인의 연산기호라고 생각하자.
축약된 형태로 Abstract Syntax를 정의해보자.
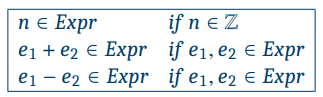

이렇게.. Abstract Syntax도 BNF 형태로 간단하게 정의할 수 있다.
Semantics
Syntax는 어떤 문장이 형식적으로 맞는 문장인가를 정의하고, Semantics는 문법적으로 올바른 문장이 실제로 어떤 의미를 가지는가를 의미한다.
Semantics를 통해 컴퓨터가 해당 코드를 어떻게 해석하고 실행해야 할 지 알 수 있다.
프로그래밍 언어에서의 Semantics는 언어에 정의된 모든 문법 구조를 의미하고,
프로그램에서의 Semantics는 어떤 프로그램이 실제로 "어떤 동작을 하는가"를 의미한다.
BNF로 작성된 Abstract Syntax를 기반으로 Semantics를 작성하자.


Semantics를 자연어로 작성할 수도 있지만..
모호하고 기계적 처리에 적합하지 않아 엄밀한 정의를 위해 Inference Rule을 도입해서 Semantics를 정의한다.
(Big Step Operation 아래 화살표 기호는 "n은 n으로 평가된다"를 의미한다)
여기서 Inference Rule은 전제로부터 결론을 이끌어내는 규칙을 의미하고,
-> 연산은 Small Step Operation으로 프로그램들의 계산이 스텝의 연속으로 수행됨을 의미한다.
정리하면..
Concrete Syntax로 작성된 코드를 파서를 통해 Abstract Syntax로 변환하고
이 Abstract Syntax를 AST로 표현할 수 있고, 이 AST에 Semantics를 부여해 코드가 실제로 뭘 의미하고 어떻게 동작해야 하는지 정의한다.
Semantics를 정의하고, 그 Semantics의 비즈니스 로직을 구현하면 인터프리터가 된다.
컴파일러, 인터프리터 개발자는 Semantics를 보고 로직을 구현한다.
⟨e1⟩ ⇓ n1 ⟨e2⟩ ⇓ n2
-----------------------
⟨Add(e1, e2)⟩ ⇓ n1 + n2
let rec eval = function
| Add (e1, e2) -> eval e1 + eval e2

평가 과정을 명확하게 표현하고 인터프리터의 기본이 되는 Proof Tree를 만들어보자.
Inference Rule을 사용해 Proof Tree를 만들어 결론을 증명한다.
일반적인 트리와 달리 Root(결론)가 최하단에 위치하고, 트리는 최하단부터 시작해 위로 차근차근 올라가는 방식으로 만들어진다.
Semantics를 사용해 특정 명제가 참임을 구조적으로 증명하는 트리.
실제로 Semantics를 적용해 숫자나 표현식을 넣고 그 결과가 맞는지 확인하는게 테스트고, 그 과정이 Proof Tree로 표현될 수 있다.
이미 정의해 둔 언어를 확장할 때는 Concrete Syntax / Abstract Syntax 모두를 수정해야 해 매우 번거롭다.
개발자는 사실상 Concrete Syntax만을 사용해서 작업하는데.. Concrete Syntax만 고치고 Abstract는 그대로 사용하는 방법은 없을까?

Syntatic Sugar는 개발자에게 편의기능을 주기 위해 도입된 기능으로, 개발자가 코드를 작성할 때는 기존과는 다른 방식으로, 마치 다른 문법이 추가된 것 처럼 작성하지만 Parser는 해당 문법으로 이전과 같은 AST를 만들어낸다.
파싱 과정에서 녹아 없어지니 Sugar... Desugaring을 수행하는 Parser의 역할이 매우 중요하다.
Syntax Sugar로 Concrete Syntax만 조작해서 새로운 문법을 만들 수 있다.
앞서 정의한 AE 언어에 Identifier 개념을 추가해 VAE 언어를 정의해보자.
Binding Occurrence : Identifier의 정의를 위해 등장한 개념으로, 변수를 정의한다.
Bound Occurrence : Identifier와 연관된 요소 사용을 위해 등장한 개념으로, 변수에 저장된 값을 사용한다.
Free Identifier : 위의 두 가지에 해당되지 않는 개념으로, 정의되지 않은 변수에 접근할 때 발생한다.

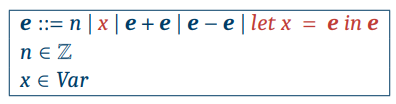

기존 언어를 확장해 expr과 Abstract Syntax를 정의하자.
변수 값을 저장하는 추상메모리는 변수를 key로, 정수를 value로 저장하는 map으로 생각할 수 있다.


추가된 추상메모리를 사용해 Semantics를 정의하고 Semantics를 Bigstep Operational Semantics로 정의하자.

같은 방식으로.. Proof Tree를 만들 수 있다.
Proof Tree가 Small Step Operation과 유사하지만.. Proof Tree에는 순서가 있지 않고, Small Step Operation은 순서가 정해져 있다.
'Computer Science > Universial Programming Language' 카테고리의 다른 글
| [UPL] Recursion (0) | 2025.05.18 |
|---|---|
| [UPL] Conditional Branch (0) | 2025.05.15 |
| [UPL] 고차원 함수와 일차원 함수 (2) | 2025.04.18 |
| [UPL] Syntax & Parsing (0) | 2025.04.04 |
| [UPL] 함수형 언어 OCaml (0) | 2025.03.21 |
댓글
이 글 공유하기
다른 글
-
[UPL] Conditional Branch
[UPL] Conditional Branch
2025.05.15 -
[UPL] 고차원 함수와 일차원 함수
[UPL] 고차원 함수와 일차원 함수
2025.04.18 -
[UPL] Syntax & Parsing
[UPL] Syntax & Parsing
2025.04.04 -
[UPL] 함수형 언어 OCaml
[UPL] 함수형 언어 OCaml
2025.03.21