[ML] Bayesian Classifier
가지고 있는 데이터셋을 사용해 모델을 학습시킨다.
여기서의 학습은 딥러닝처럼 파라미터 최적화가 아니라 확률 분포를 추정하는 과정으로 확률 테이블을 만든다고 생각하자.
이제 새로운 데이터가 들어오면 베이즈 정리를 사용해 사후 확률을 계산한다.
모든 클래스에 대해 확률을 계산하고 가장 큰 확률을 가지는 클래스로 데이터를 분류한다.
\[
P(w_j \mid x) = \frac{P(x \mid w_j) \, P(w_j)}{P(x)}
\]
$$
P(w_j) \quad
\begin{array}{l}
\text{Prior: 데이터를 보기 전에 해당 클래스가 나타날 확률을 의미한다.} \\
\text{새로운 데이터를 보기 전 기본적인 기대치 역할을 한다.}
\end{array}
$$
$$
p(x \mid w_j) \quad
\begin{array}{l}
\text{Likelihood: 해당 클래스가 참일 때 발생할 조건부 확률을 의미한다.} \\
\text{클래스의 데이터 생성 분포/모수에 의해 결정되고, 데이터가 해당 클래스에} \\
\text{얼마나 잘 어울리는지 보여준다.}
\end{array}
$$
$$
p(x) = \sum_{k} p(x \mid w_k)\,P(w_k) \quad
\begin{array}{l}
\text{Evidence: 관찰된 데이터 $x$가 등장할 모든 확률을 의미한다.}
\end{array}
$$
분류 문제에서는 값 자체보다는 어떤 값이 더 큰지가 더 중요하다.
그러니 분모는 어차피 같으니 계산에 중요하지 않다. 크기만 비교하면 된다.
모델링 대상을 구분할 때는 Generative와 Discriminative 방식을 사용한다. - 무엇을 학습할지?
Generative - 데이터가 어떻게 생성되는지를 모델링한다. (클래스의 분포 / 사전확률을 학습)
즉 학습한 내용을 바탕으로 Posterior를 계산하는 전형적인 접근방법이다.
이론은 정확하게 계산하는게 맞는데 사실 데이터의 정확한 분포를 알 수 없으니 근사 때리고 모델링한다.
joint distribution을 모델링
Discriminative - 데이터가 어떻게 생성되는지는 무시하고 바로 boundary와 조건부 확률을 학습한다.
어차피 분류 할 때는 Posterior의 크기만 비교하면 되니까 Posterior를 정확하게 계산하지 않아도 된다.
목표는 두 개체를 분리하는 함수를 얻는 것.
conditional distribution을 모델링
$$
g_i(x) = P(w_i \mid x) \propto P(x \mid w_i) P(w_i) \quad
\begin{array}{l}
\text{클래스 $w_i$의 판별 함수 $g_i(x)$를 정의한다.} \\
\end{array}
$$
$$
g_i(x) = \ln P(x \mid w_i) + \ln P(w_i) \quad
\begin{array}{l}
\text{로그 함수는 단조 증가 함수이므로 클래스 선택 결과에 영향을 주지 않는다.} \\
\text{곱을 합으로 바꿀 수 있어 계산과 표현이 단순해진다.}
\end{array}
$$
$$
\text{Decision boundary: } \quad g_1(x) = g_2(x) \quad
\begin{array}{l}
\text{결정 경계는 두 클래스의 판별 함수 값이 동일한 지점들의 집합이다.} \\
\text{즉, 어느 쪽도 우세하지 않은 지점이 바로 경계가 된다.}
\end{array}
$$
$$
g(x) = g_1(x) - g_2(x) = 0 \quad
\begin{array}{l}
\text{두 클래스의 점수 차이를 하나의 함수 $g(x)$로 묶어 표현한다.} \\
\text{$g(x) > 0$이면 $w_1$, $g(x) < 0$이면 $w_2$로 분류한다.} \\
\text{$g(x) = 0$인 지점이 바로 결정 경계이다.}
\end{array}
$$
$$
g(x) = \big( \ln P(x \mid w_1) + \ln P(w_1) \big)
- \big( \ln P(x \mid w_2) + \ln P(w_2) \big) = 0 \quad
\begin{array}{l}
\text{베이즈 정리에서 유도된 식에 로그를 취한 형태이다.} \\
\text{곱이 합으로 바뀌어 다루기 쉬워지고, 미분하기도 쉽다.} \\
\end{array}
$$
Parameter Estimation
Prior과 Likelihood를 정확하게 알고 있다면 분류기를 만들 수 있지만, 현실적으로 데이터의 진짜 분포를 알기 어렵다.
따라서 특정 분포 모형을 가정하고, 그 파라미터를 데이터로부터 추정하는 방식이 Parameter Estimation 이다.
여기서 Parameter는 확률 분포를 정의하는 숫자를 의미한다. (평균, 분산)
Parameter Estimation의 방식으로는 두 가지가 있다. - 어떻게 학습할지?
Parametric - 분포를 가정한다. 가우시안 분포를 따른다고 가정한다던지.. 가정한 후 파라미터인 평균, 분산을 추정한다.
Non-Parametric - 분포 형태를 가정하지 않고 데이터 자체로 추정한다. (모델 자체에 대한 추정)
$$
P(x) = \frac{1}{\sqrt{2\pi}\,\sigma}
\exp\left( -\frac{1}{2} \left( \frac{x - \mu}{\sigma} \right)^2 \right)
\quad
\begin{array}{l}
\text{Univariate Gaussian (1차원 정규분포)} \\
\text{$\mu$: 평균, $\sigma^2$: 분산} \\
\text{특징이 하나일 때 사용한다.}
\end{array}
$$
$$
P(x) = \frac{1}{(2\pi)^{d/2} \, |\Sigma|^{1/2}}
\exp\left( -\frac{1}{2} (x - \mu)^T \Sigma^{-1} (x - \mu) \right)
\quad
\begin{array}{l}
\text{Multivariate Gaussian (다변량 정규분포)} \\
\text{$\mu$: 평균 벡터, $\Sigma$: 공분산 행렬} \\
\text{특징이 여러 개인 경우 사용.}
\end{array}
$$
$$
g_i(x) = -\frac{1}{2} (x - \mu_i)^T \Sigma_i^{-1} (x - \mu_i)
- \frac{d}{2} \ln(2\pi)
- \frac{1}{2} \ln |\Sigma_i|
+ \ln P(w_i)
\quad
\begin{array}{l}
\text{Gaussian 분포를 가정한 베이즈 분류기의 판별함수(discriminant function)} \\
\mu_i : \text{클래스 $w_i$의 평균 벡터} \\
\Sigma_i : \text{클래스 $w_i$의 공분산 행렬} \\
d : \text{특징 벡터의 차원} \\
P(w_i) : \text{클래스 $w_i$의 사전확률}
\end{array}
$$
즉, 흐름을 정리해보면..
Bayesian Classifier의 수식은 간단하지만, 실제로 사용하려면 Likelihood를 알아야 Posterior를 계산할 수 있고, 현실에서는 저 분포를 정확하게 알 수 없다.
그러니 분포를 추정해야 하니 Parameter Estimation을 사용한다.
여기서 자주 사용하는 분포가 Gaussian Distribution이고, 1차원 피쳐인 경우 평균 + 분산만 사용하고 다차원이면 평균벡터 + 공분산행렬을 사용한다.
비교가 목적이니까 로그를 씌워도 동일한 결과를 얻는다. 계산은 단순해지고 수치가 안정적으로 변한다.
분포는 추정하더라도 그 분포의 파라미터인 평균, 분산은 실제 데이터를 통해 가져와야 한다.
여기서 데이터를 가장 그럴듯하게 설명하는 파라미터를 찾기 위해 Maximum Likelihood Estimation 을 사용한다.
$$
P(x \mid \omega_j) \sim \mathcal{N}(\mu_j,\Sigma_j),
\qquad P(x \mid \omega_j) \equiv P(x \mid \omega_j, \theta_j)
\quad
\begin{array}{l}
\text{클래스 } \omega_j \text{의 likelihood를 가우시안으로 가정한다.}\\
\theta_j = (\mu_j,\Sigma_j): \text{추정할 파라미터(평균벡터, 공분산행렬).}
\end{array}
$$
$$
P(D \mid \theta) = \prod_{k=1}^{n} P(x_k \mid \theta) \quad
\begin{array}{l}
\text{데이터 } D=\{x_1,\dots,x_n\} \text{가 } \theta \text{에서 관측될 우도(likelihood).}\\
\text{각 클래스가 독립적이고 동일한 분포를 가진다는 가정 하에 개별 확률의 곱으로 쓴다.}
\end{array}
$$
$$
\hat{\theta}_{\mathrm{MLE}} = \arg\max_{\theta} P(D \mid \theta) \quad
\begin{array}{l}
\text{Likelihood를 최대화하는 } \theta \text{가 MLE 추정치이다.}
\end{array}
$$
$$
\ell(\theta) = \ln P(D \mid \theta) = \sum_{k=1}^{n} \ln P(x_k \mid \theta) \quad
\begin{array}{l}
\text{로그-우도: 곱 } \to \text{ 계산 오류 방지 및 미분을 쉽게}
\end{array}
$$
$$
\nabla_{\theta}\,\ell(\theta) = \sum_{k=1}^{n} \nabla_{\theta}\,\ln P(x_k \mid \theta) \quad
\begin{array}{l}
\text{최대화 조건: } \nabla_{\theta}\,\ell(\hat{\theta}) = 0 \
\end{array}
$$
$$
\ln P(x_k \mid \mu)
= -\frac{1}{2}\ln\!\big((2\pi)^d|\Sigma|\big)
-\frac{1}{2}(x_k-\mu)^{\!T}\Sigma^{-1}(x_k-\mu)
$$
$$
\nabla_{\mu}\,\ln P(x_k \mid \mu)
= \Sigma^{-1}(x_k-\mu)
\quad\Rightarrow\quad
\nabla_{\mu}\,\ell(\mu)
= \sum_{k=1}^{n} \Sigma^{-1}(x_k-\mu) = 0
$$
$$
\hat{\mu} = \frac{1}{n}\sum_{k=1}^{n} x_k \quad
\begin{array}{l}
\text{즉, MLE 평균은 샘플 평균과 같다.}
\end{array}
$$
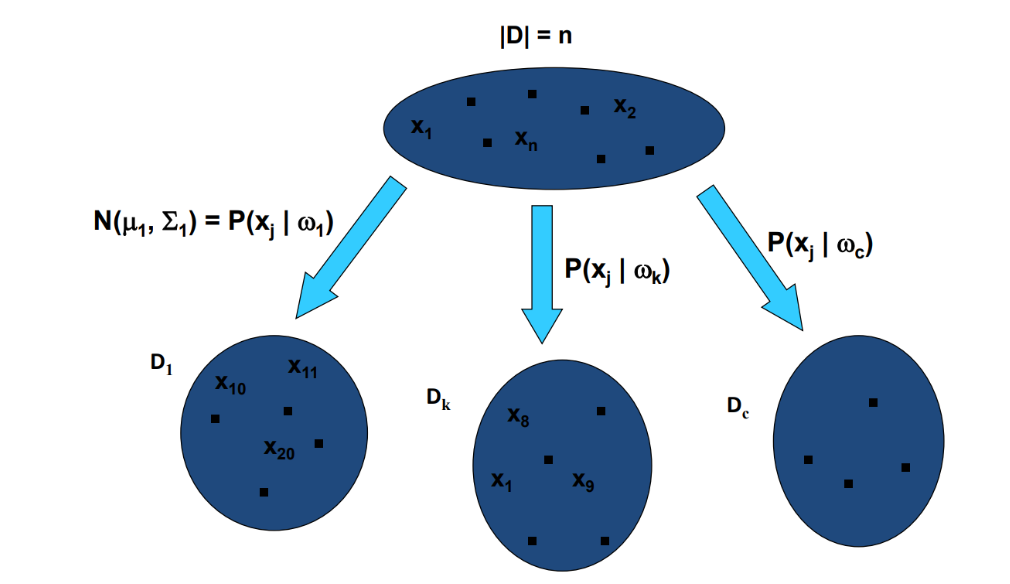
데이터셋 D를 클래스별로 나누고 각 클래스 데이터셋을 기반으로 MLE를 사용해 가우시안 분포를 추정한다.
이제 새로운 입력 x가 들어오면 추정해둔 각 클래스별 확률분포를 계산하고, Posterior를 구해서 가장 큰 값을 가지는 클래스로 분류한다.
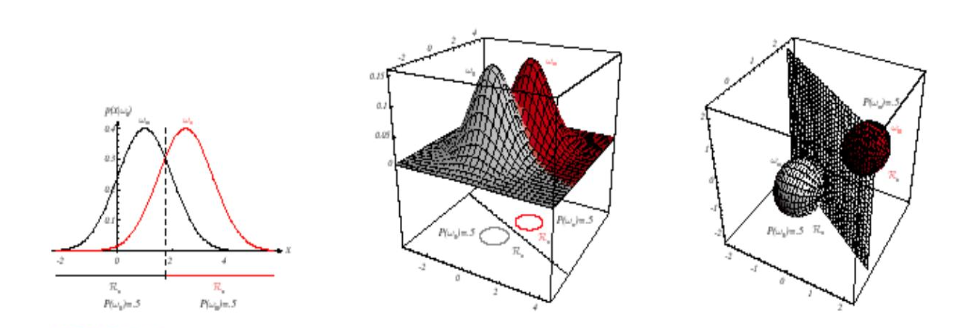
데이터 feature의 개수에 따라 결정 경계가 형성되는 위치가 달라진다.
feature의 개수 d가 늘어날수록 공분산 행렬의 크기가 커진다. (d*d)
샘플 수가 충분하지 않으면 공분산 추정이 불안정해지고 학습 효율이 낮아지니 고차원 데이터에서는 Naive Bayesian Classifier를 사용한다.
모든 feature가 독립이라고 가정해 공분산을 만들지 않아도 되고, 각 feature간의 분산만 추정하면 되니 계산이 매우 간단하다.
당연히 현실적으로 모든 feature가 독립일 경우는 거의 없으니 모델의 정확도는 떨어진다.
$$
P(w_j \mid x) = \frac{P(x \mid w_j) \, P(w_j)}{P(x)} \quad
\begin{array}{l}
\text{베이즈 정리 - Posterior = Likelihood × Prior / Evidence}
\end{array}
$$
$$
P(x \mid w_j) = P(x_1, x_2, \ldots, x_d \mid w_j) \quad
\begin{array}{l}
\text{일반적으로는 모든 feature joint 분포를 추정}
\end{array}
$$
$$
P(x \mid w_j) \approx \prod_{i=1}^d P(x_i \mid w_j) \quad
\begin{array}{l}
\text{Naive 가정: feature들이 조건부 독립 가정}
\end{array}
$$
$$
P(w_j \mid x_1, x_2, \ldots, x_d)
= \frac{\prod_{i=1}^d P(x_i \mid w_j)\,P(w_j)}{P(x)} \quad
\begin{array}{l}
\text{최종 Naive Bayes 분류 공식}
\end{array}
$$
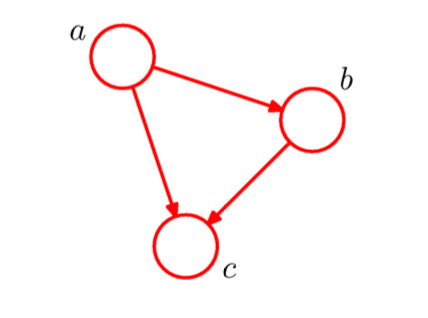
모든 feature 가 다 독립이라고 가정하기보다는 실제 의존 구조만 반영하는 모델이 Bayesian Belief Network이다.
변수들의 확률적 관계를 DAG로 정의해 누가 누구에게 영향을 주는지를 표현한다.
변수 자체의 확률분포를 작은 조건부확률들의 곱으로 분해한다.
$$
P(a,b,c) = P(c \mid a,b) \, P(b \mid a) \, P(a)
\quad
$$
$$
P(x_1, x_2, \dots, x_k) = \prod_{i=1}^{k} P(x_i \mid pa(x_i))
\quad
$$
$$
P(r,w,c,h,b) = P(r)\,P(w \mid r)\,P(c \mid r)\,P(h \mid w,r)\,P(b \mid w,c)
\quad
$$
$$
P(\omega_i \mid x, D) =
\frac{P(x \mid \omega_i, D)\,P(\omega_i \mid D)}
{\sum_{j=1}^{c} P(x \mid \omega_j, D)\,P(\omega_j \mid D)}
\quad
$$
$$
P(\omega_i \mid x) =
\frac{P(x \mid \omega_i)\,P(\omega_i)}
{\sum_{j=1}^{c} P(x \mid \omega_j)\,P(\omega_j)}
\quad
$$
결과값은 수치로 된 값이 아니고 클래스이다. 몇 가지 클래스가 미리 주어지고, 새로운 입력에 대해 그 입력이 어떤 클래스에 속하는지 알아낼 때 사용한다.
Salmon과 Sea Bass를 구분한다고 하면.. 일단 이미지니까 여러 가지 시각적 특징을 활용한다.
Width, Lightness 등.. 특징을 벡터라고 두면 데이터셋은 행렬로 표현할 수 있다.
이제 구하는 건, 입력 x 가 주어졌을 때 이게 어떤 클래스 w에 속하는지를 검사하는 것.
여기서 값은 중요하지 않다. w1보다 w2가 크다면 x는 w2에 속한다고 판단할 수 있으면 되니까, 누가 더 큰지가 중요하다.
이제부터는 그냥 조건부확률 구하기...
<구해야 하는 것>
그냥 아무거나 잡았을 때 이게 Salmon일 확률, Bass일 확률 - Prior
Bass일 때 Width가 일정 수치보다 클 확률, Salmon일 때 Lightness가 일정 수치보다 클 확률 - Likelihood
전체 물고기 중 지금 이 특징을 가진 물고기가 나올 확률 - Evidence
Prior Likelihood Evidence를 구한 이유는, 결국 x가 주어졌을 때 어떤 클래스 w에 속하는지 알기 위해서이다.
즉, Posterior를 구하기 위해서이다.
사실 Evidence는 정규화를 위해서만 필요한거니까.. 크기 비교만 할 때는 필요 없다.
그래도 크기 비교만 할 때 여도 Likelihood 계산을 위해 Parametric Estimation 은 필요하다.
이제 구하는건 끝났고.. 오류를 계산해야 한다.
입력 x 에 대해 이게 w1이라고 생각했는데 사실 w2였고, w2라고 생각했는데 사실 w1일 수 있다.
연어라고 생각했는데 농어일 확률 = P(w1 | x)
농어라고 생각했는데 연어일 확률 = P(w2 | x)
오류 확률은 둘 중 더 작은 쪽으로 선택한다.
현실은 Prior Likelihood Evidence 정확히 구할 수 없다. 그러니 Parametric Estimation을 사용해 추정하거나, 다른 방법을 사용한다.
Parametric Estimation
연어, 농어 데이터를 많이 모으면 이게 어떤 모델인지 추정할 수 있다.
Generative Model은 각 클래스의 데이터 분포 자체를 모델링하는거고,
Discriminative Model은 클래스의 구분 경계만 찾는걸 의미한다.
데이터의 분포 형태는 미리 가정해둔다. Gaussian을 가정하거나.. Exponential을 가정하거나..
실제로 관측된 데이터가 가장 잘 나올 수 있게 만드는 확률분포의 파라미터를 찾기 위해 MLE를 계산한다.
Non-Parametric Estimation
모델 형태를 구하지 않고 데이터로 근사하는 방식이다.
데이터 자체를 모델로 보고, 데이터 분포를 직접 근사 때려버린다.
'Computer Science > Machine Learning' 카테고리의 다른 글
| [ML] Logistic Regression (0) | 2025.10.17 |
|---|---|
| [ML] Regression (0) | 2025.10.17 |
| Pytorch Lightning (0) | 2022.03.26 |
| Pytorch / Tensorflow - 차원 (0) | 2022.03.18 |
| Pytorch - Tensor (0) | 2022.03.16 |
댓글
이 글 공유하기
다른 글
-
[ML] Logistic Regression
[ML] Logistic Regression
2025.10.17 -
[ML] Regression
[ML] Regression
2025.10.17 -
Pytorch Lightning
Pytorch Lightning
2022.03.26 -
Pytorch / Tensorflow - 차원
Pytorch / Tensorflow - 차원
2022.03.18