[ML] Logistic Regression
Linear Regression과 매우 유사하지만 output이 수치가 아니라 클래스이다.
Linear Regression은 Least Square Estimation을 사용하지만 Logistic Regression은 Maximum Likelihood Estimation 사용.
Feature를 선형결합하는건 맞는데, 그 값을 확률로 바꾸기 위해 Sigmoid 함수를 사용한다.
값이 확률이 됐으니 그 확률이 미리 정해둔 임계값과 비교해서 지금 들어온 input이 어떤 클래스인지 분류한다.
일단 선형함수는 음의 무한에서 양의 무한까지의 값을 가질 수 있으니, 이걸 0~1 사이의 확률로 바꿔야 한다.
이 때 사용하는 변환 함수는 Monotonic Increasing 성질을 만족해야 하는데, 그 함수 중 하나가 Sigmoid 함수.
왜 단조증가? - 입력이 커질수록 발생할 확률이 늘어나는 식으로 모델링 해야 하기 때문 ..
Sigmoid 함수를 역함수 때리면 log odds 식이 나온다.
그러니까.. Logistic Regression은 Linear Regression + Classification이라고 보면 된다.
학습을 통해 로지스틱 회귀의 매개변수를 계산해놓으면
입력값 X가 n만큼 증가할 때 예측값이 m만큼 증가함을 알 수 있다. Linear Regression처럼 결과 해석이 간단하지 않다.
Binary Classification을 가정하면 출력 y는 베르누이 분포를 따른다.
베르누이 분포를 가정하고 MLE를 추정하면, 추정해야 하는 매개변수는 가중치 벡터가 된다.
Classifier에서 다뤘듯 Likelihood는 각 입력 X에서 Y=1 일 확률을 예측한다.
우도 함수는 현제 파라미터에서 이 데이터가 나올 확률을 의미하게 된다. 데이터가 여러 개 있으니 각 데이터의 확률을 모두 곱한다.
MLE에서는 최대가 되는 파라미터를 찾는다. 계산의 편의를 위해 로그를 씌워서 로그우도로 바꿔서 계산한다.
식이 비선형이기에 미분해서 0 되는 지점을 찾는 방식으로 최대를 구하는게 힘들다. 수치적 최적화 방법을 쓰자.
Cross Entropy는 실제 데이터 분포 P와 모델 분포 Q가 있을 때 Q가 P에 맞춰서 기술할 때 평균 몇 비트가 드는지를 의미한다.
당연히 Q가 P에 잘 맞을수록 H(P,Q)는 작아진다.
식을 잘 정리 해 보면.. MLE로 구한 cost function은 CE의 식과 동일함을 확인할 수 있다.
클래스를 예측할 때는 세 가지 경우로 나뉜다.
1. Binary Classification - 말 그대로 둘 중 하나로 분류
2. Multiclass Classification - 클래스가 3개 이상일 때 그 중 하나로 분류
3. Multilabel Classification - 데이터가 여러 클래스에 동시에 속할 수 있음
Multiclass Classification 에서는 다른 클래스에 대한 거리가 동일하게 순서를 매겨 줘야 한다.
그러니 one-hot encoding 방식을 사용해 클래스를 구분한다.
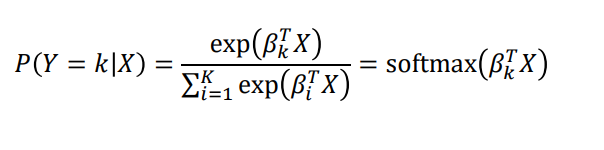
또, 각 클래스의 확률이 음수가 될 수 없고, 합은 1로 정해져있다.
이를 보장하기 위한 가장 자연스러운 파라미터 함수가 Softmax이다.
Classification에 대한 성능을 측정할 때, 이전까지는 accuracy와 misclassification만 체크했었다.
하지만 판단 오류의 cost는 생각보다 더 크다.
암을 진단하는 경우, 실제로는 암인데 암이 아니라고 진단하는 경우가 훨씬 더 치명적이다.

그래서 이 Confusion Matrix가 도입됐다.
이 행렬을 사용해 Accuracy / Precision / Recall / Recall / Specific / False Alarm 등 여러 지표를 계산한다.
'Computer Science > Machine Learning' 카테고리의 다른 글
| [ML] Decision Tree (0) | 2025.10.18 |
|---|---|
| [ML] Nearest Neighbor Method (0) | 2025.10.18 |
| [ML] Regression (0) | 2025.10.17 |
| [ML] Bayesian Classifier (0) | 2025.09.22 |
| Pytorch Lightning (0) | 2022.03.26 |
댓글
이 글 공유하기
다른 글
-
[ML] Decision Tree
[ML] Decision Tree
2025.10.18 -
[ML] Nearest Neighbor Method
[ML] Nearest Neighbor Method
2025.10.18 -
[ML] Regression
[ML] Regression
2025.10.17 -
[ML] Bayesian Classifier
[ML] Bayesian Classifier
2025.09.22